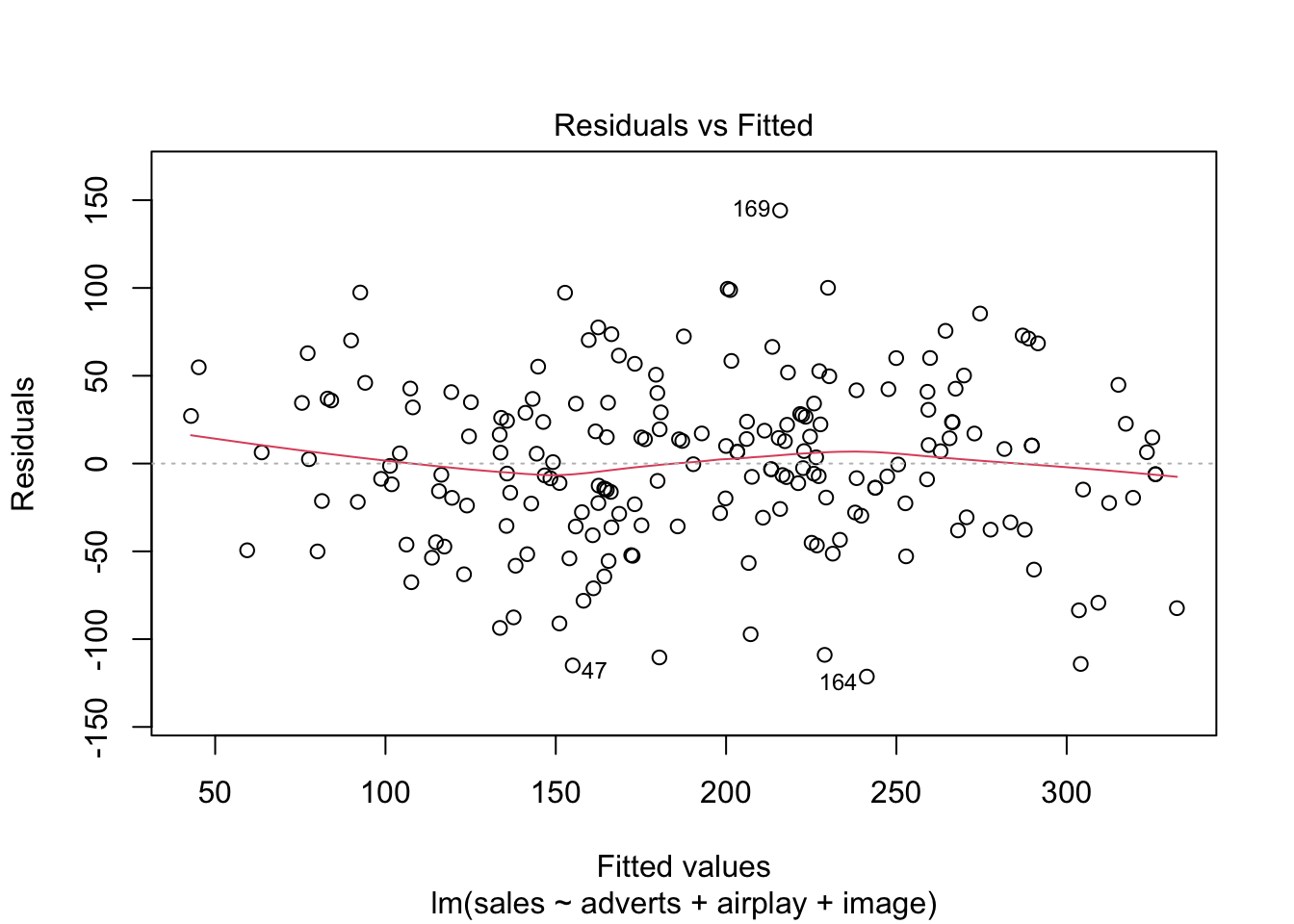
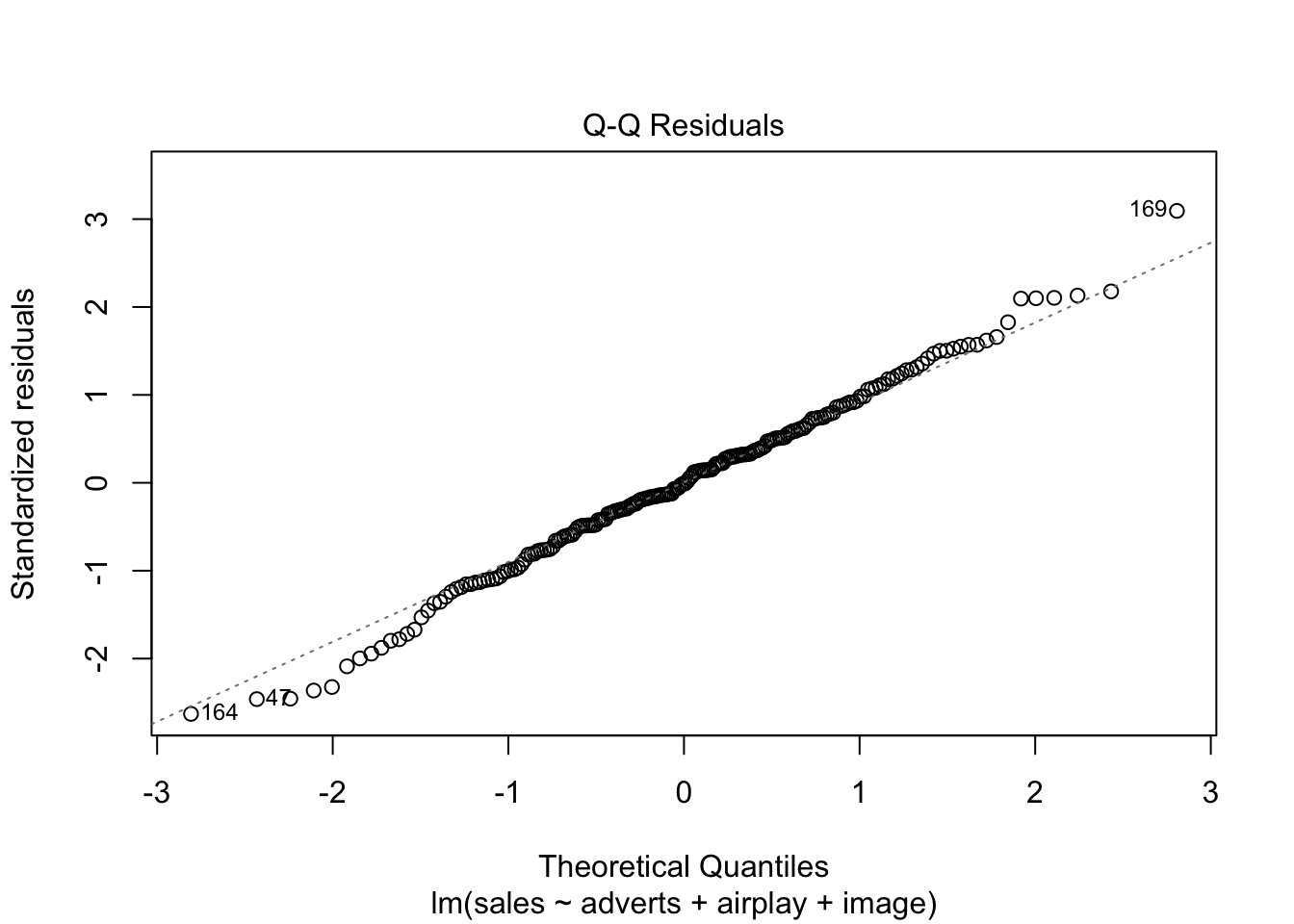
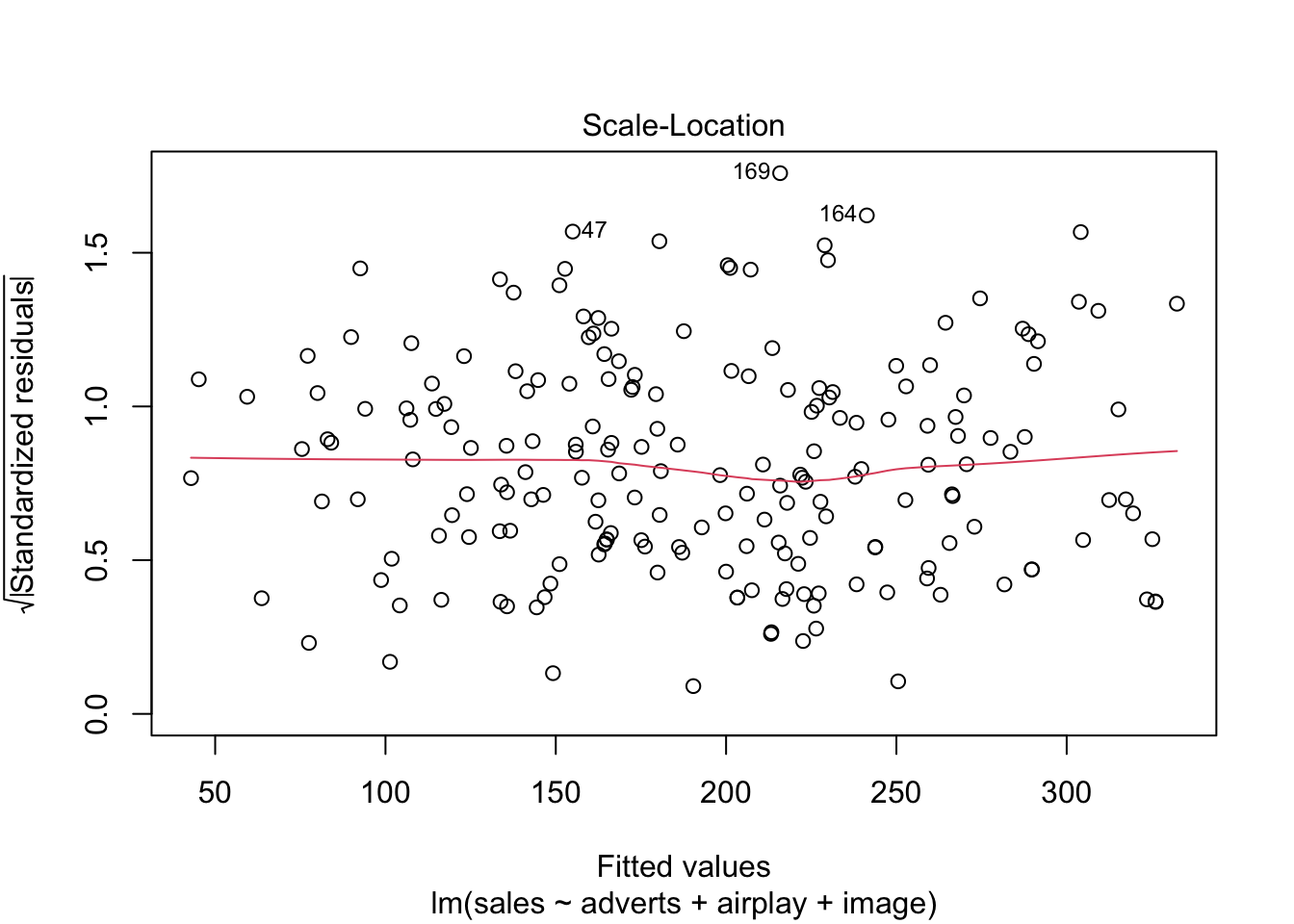
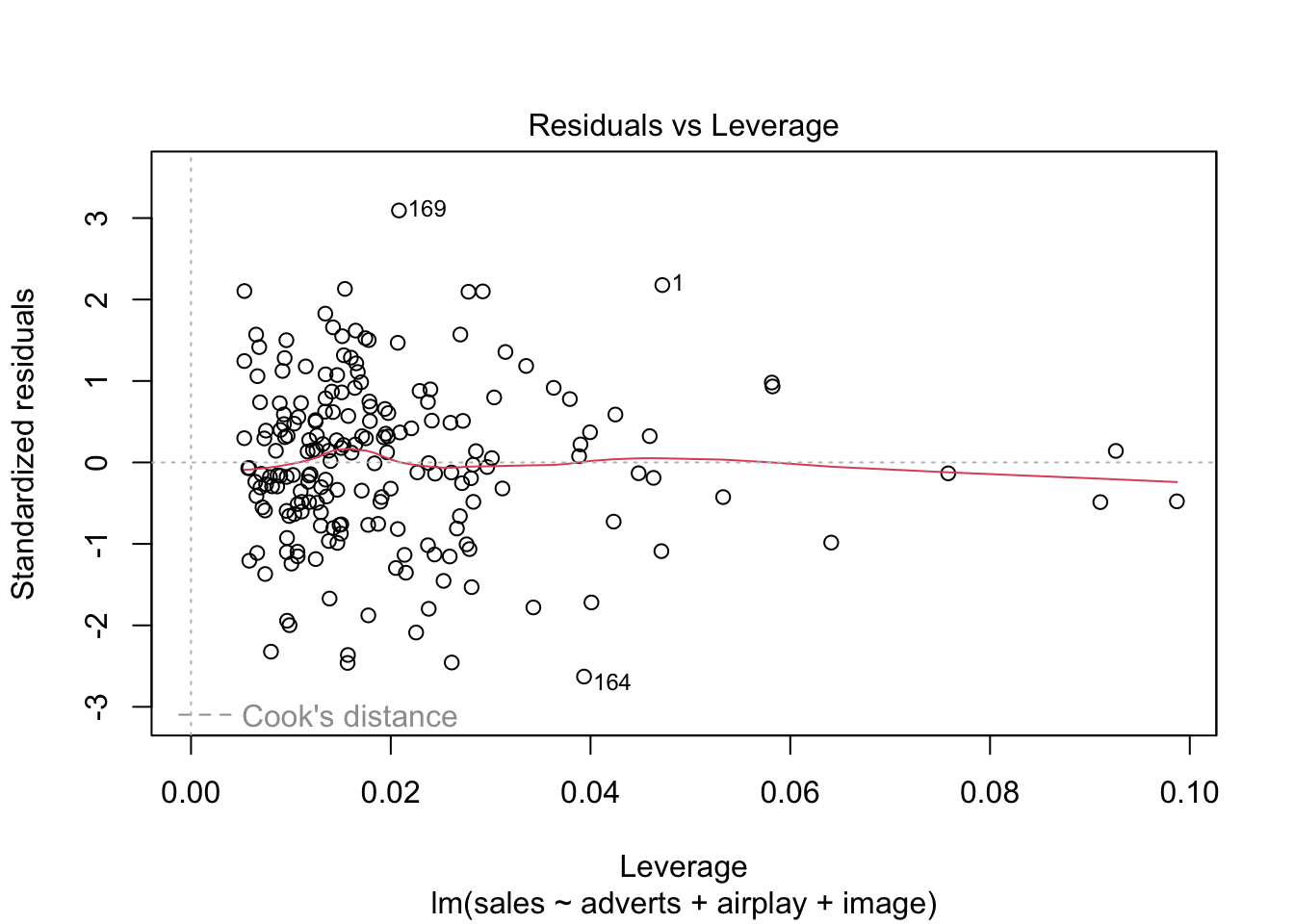
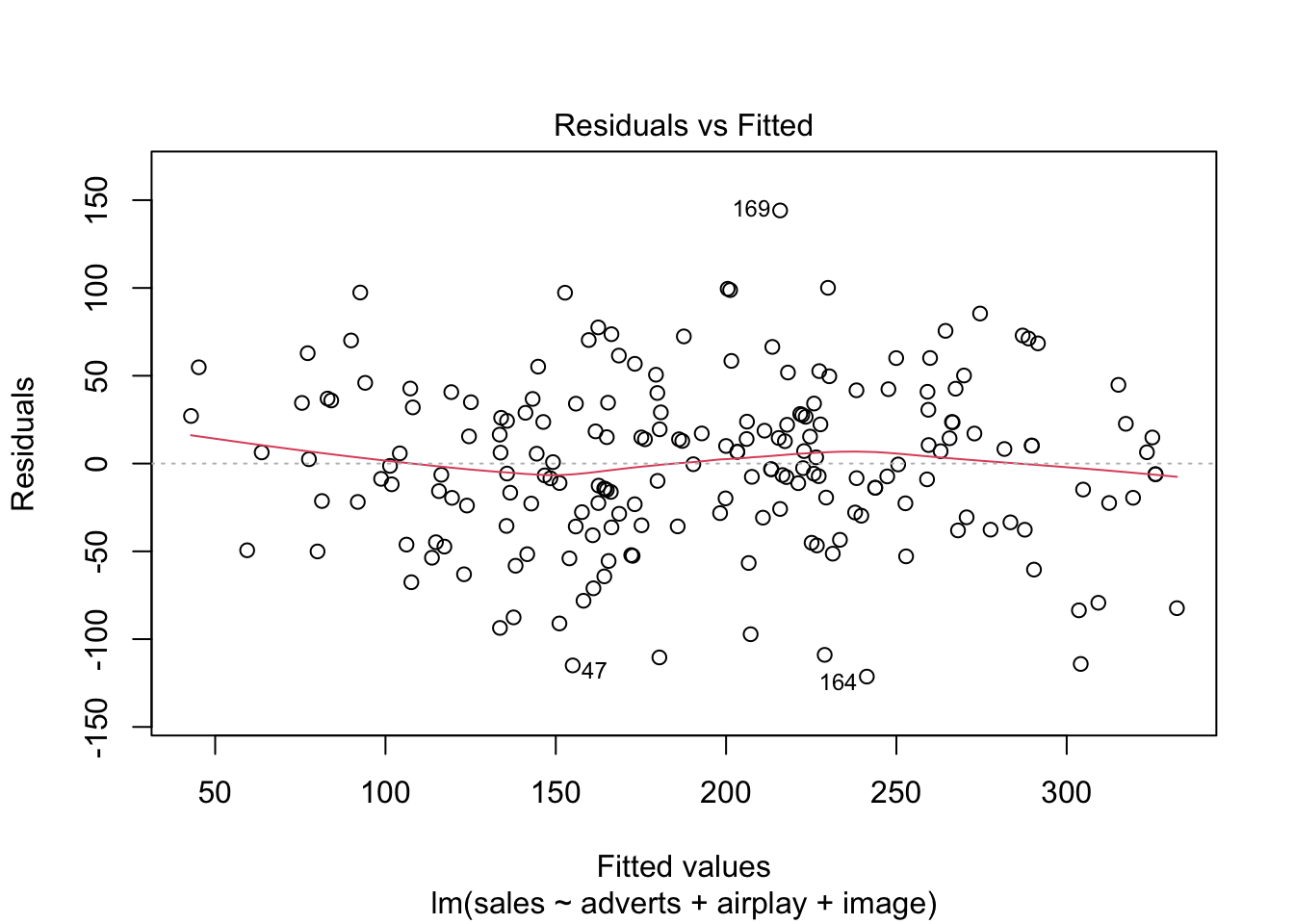
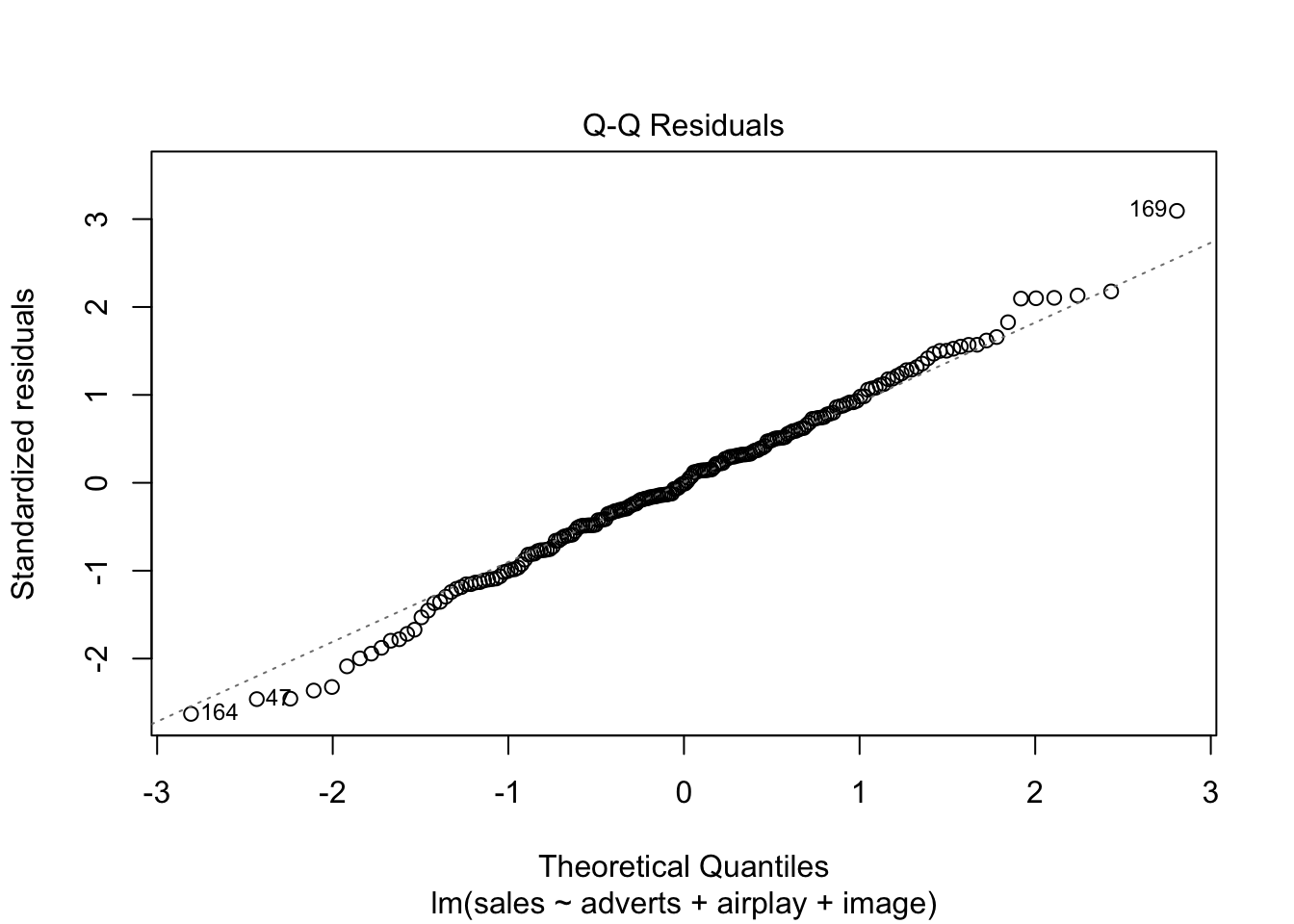
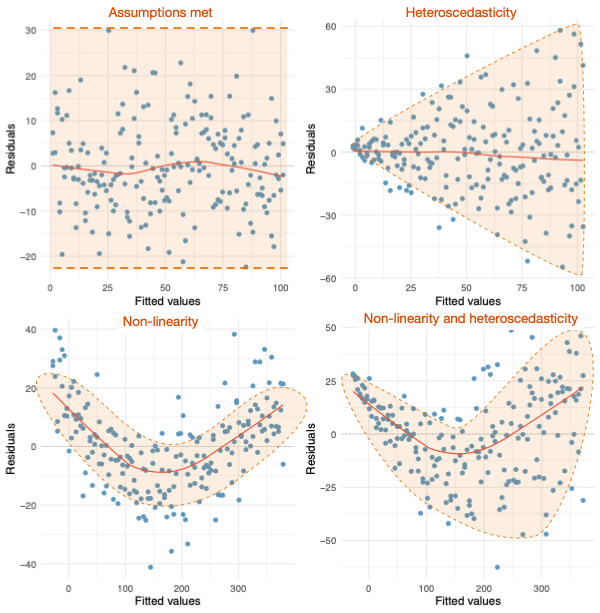
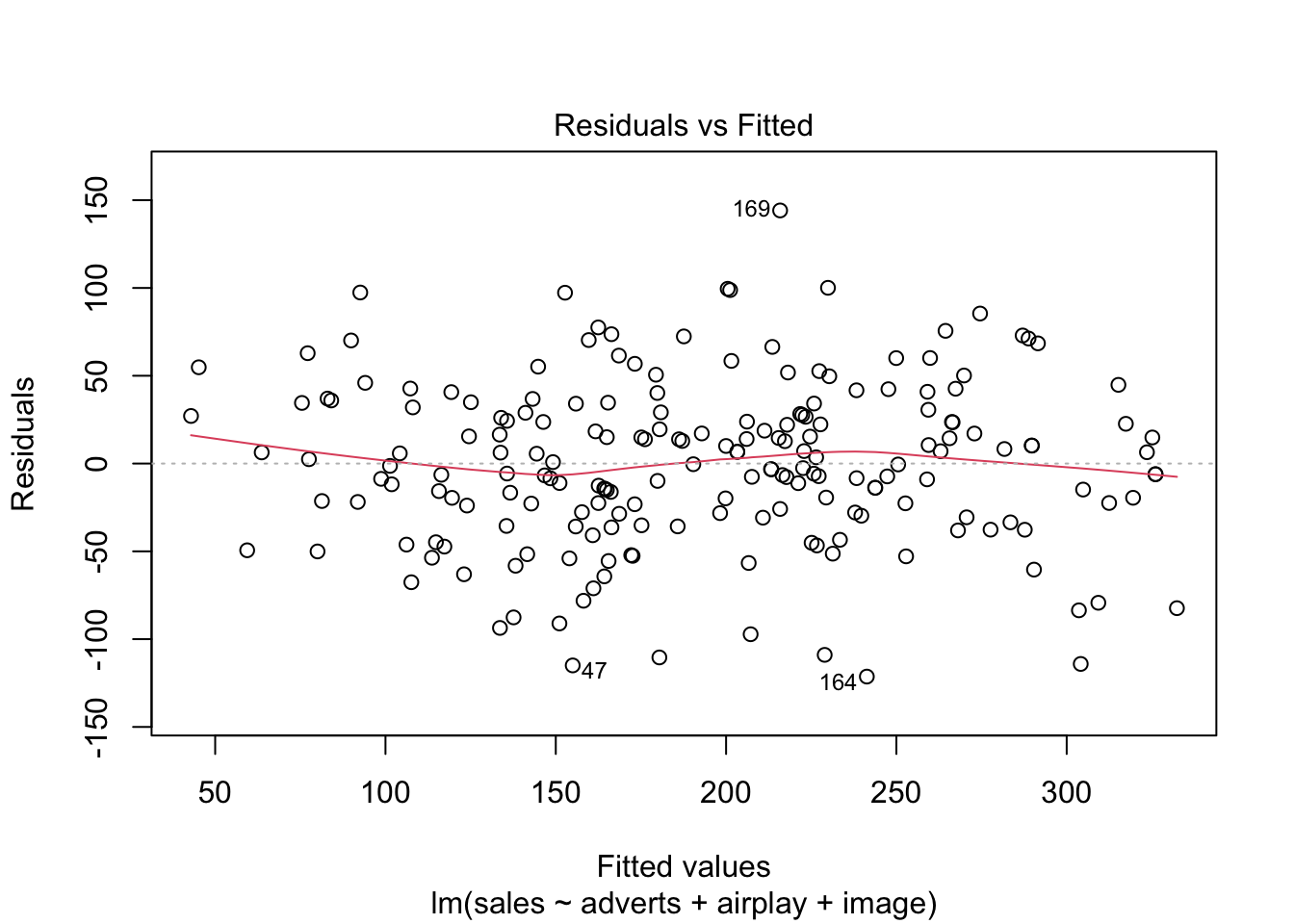
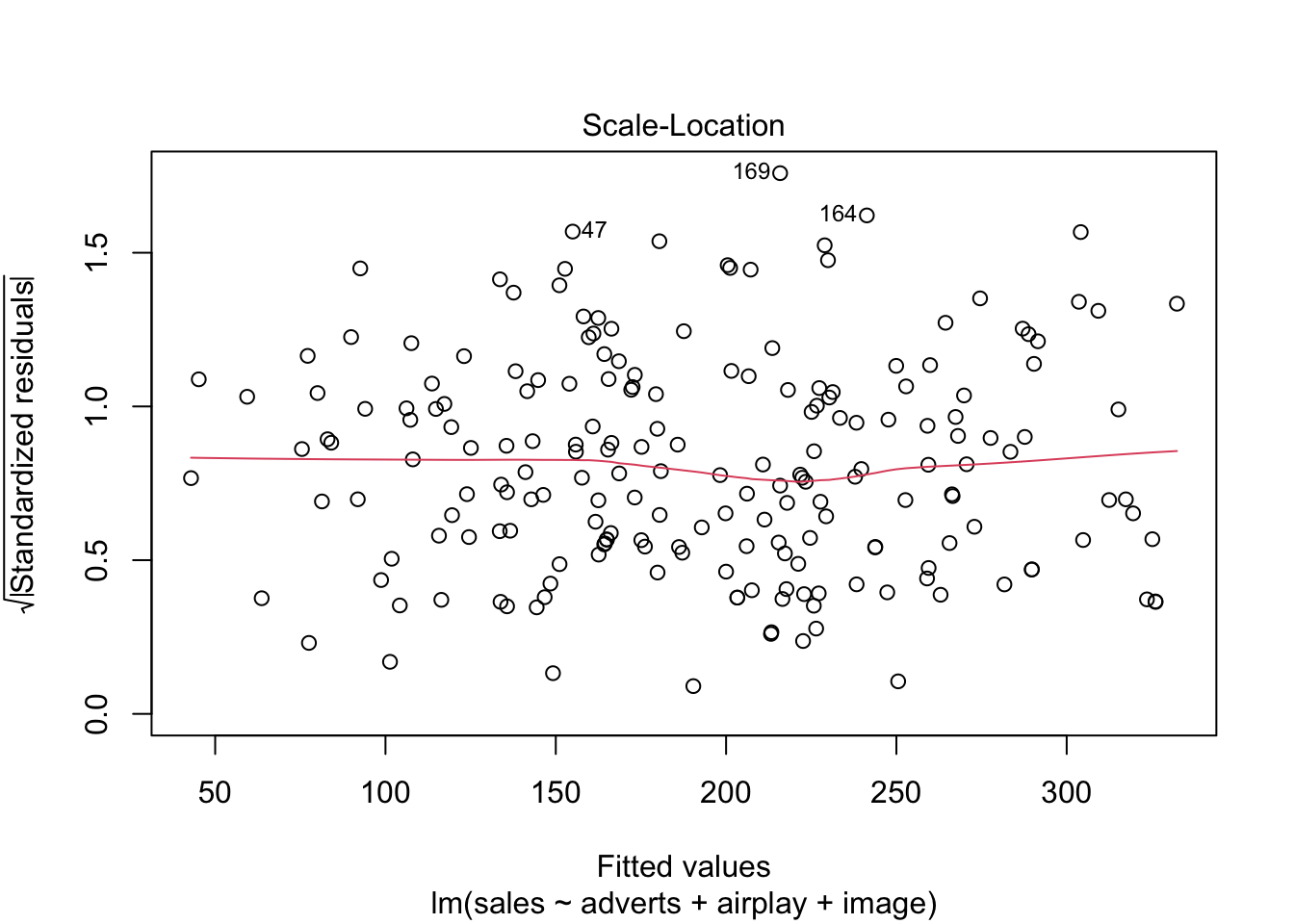
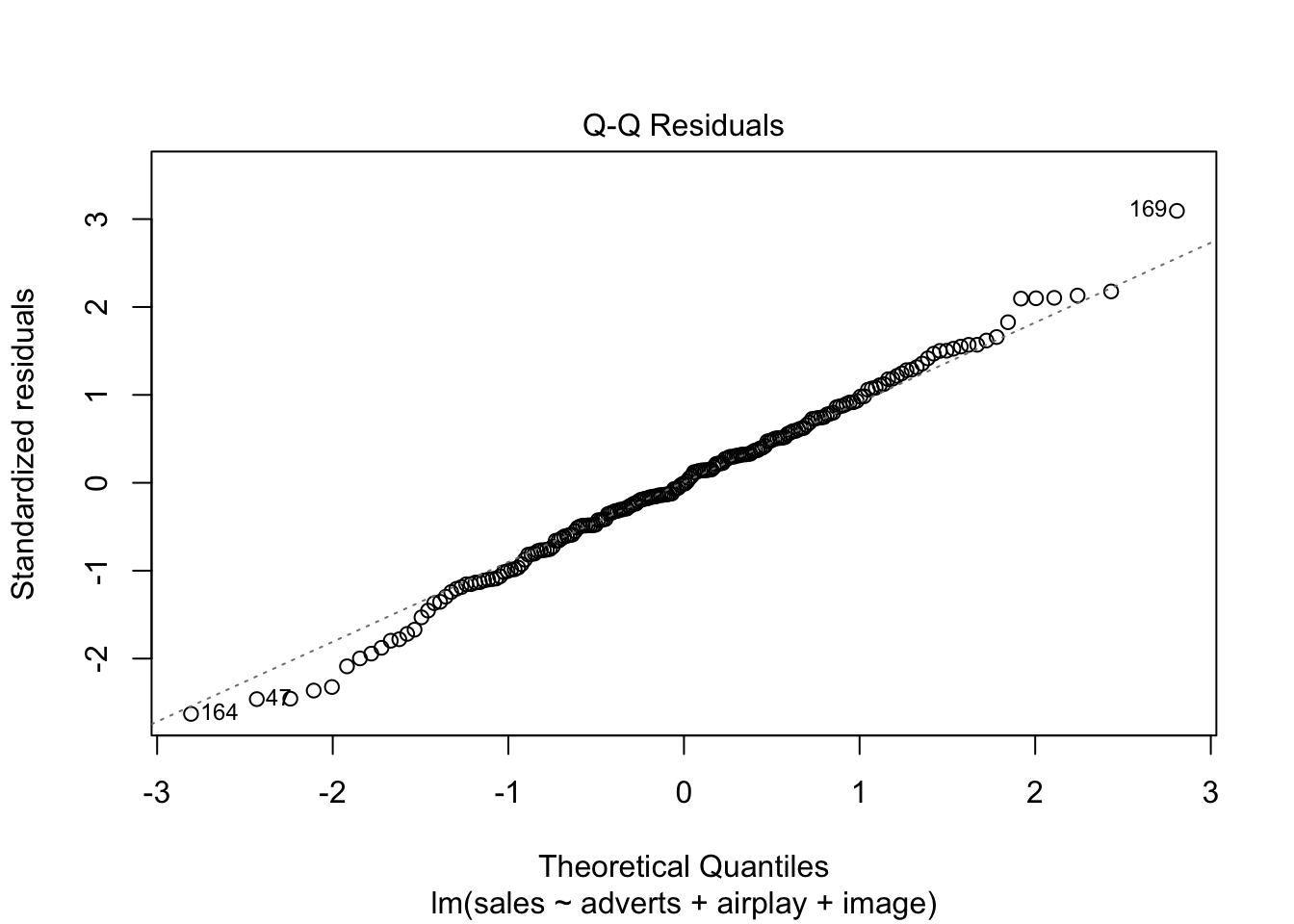
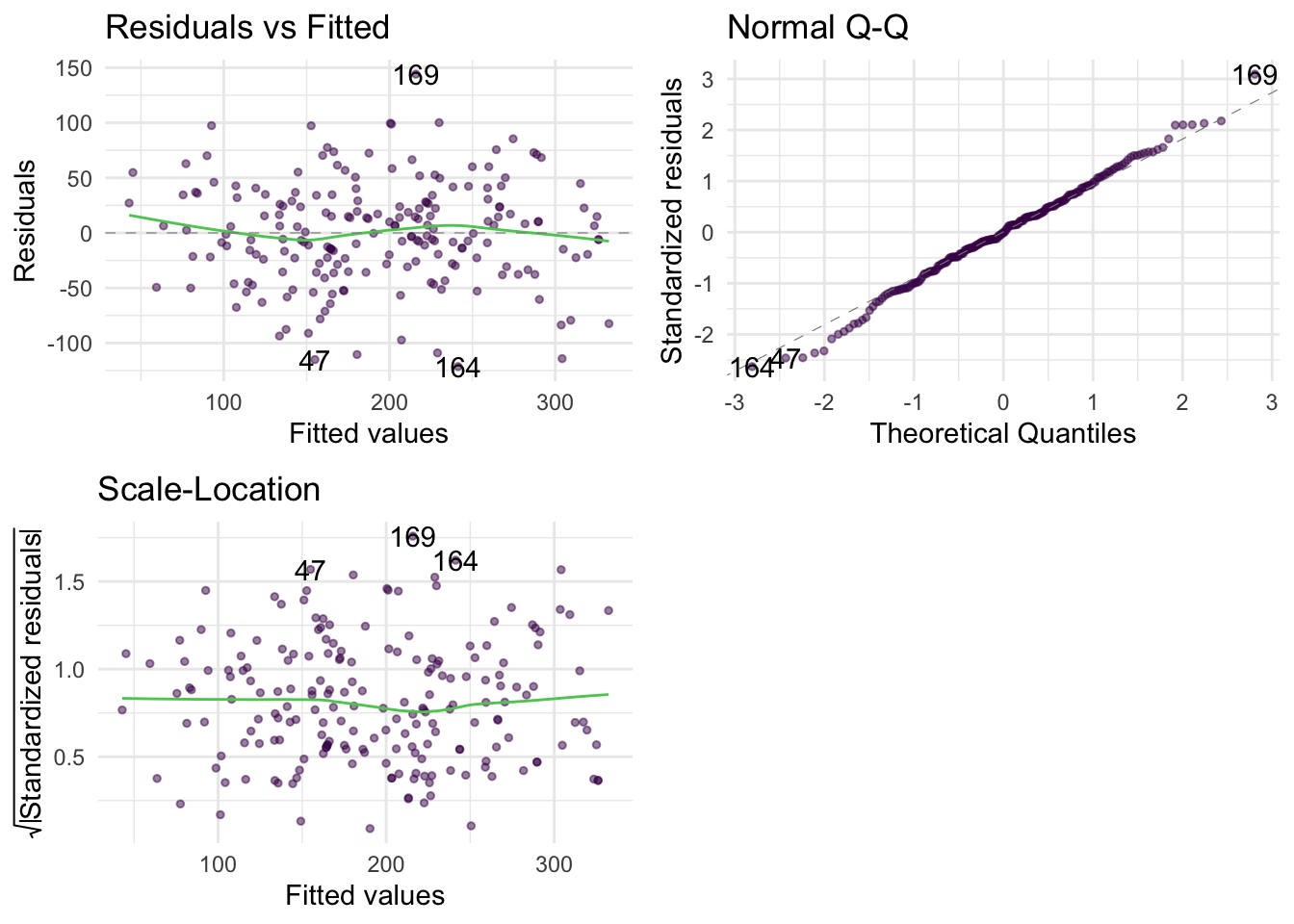
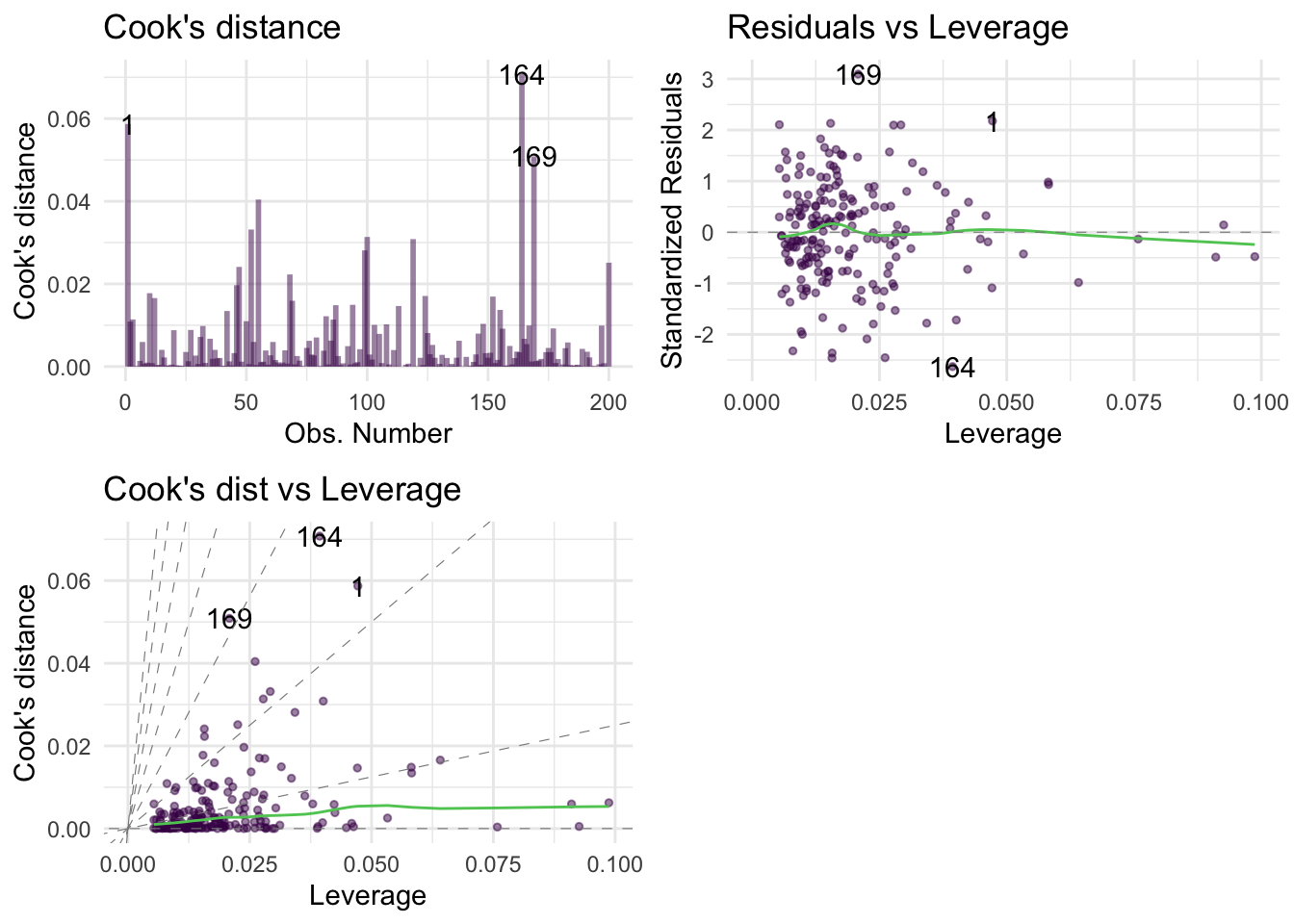
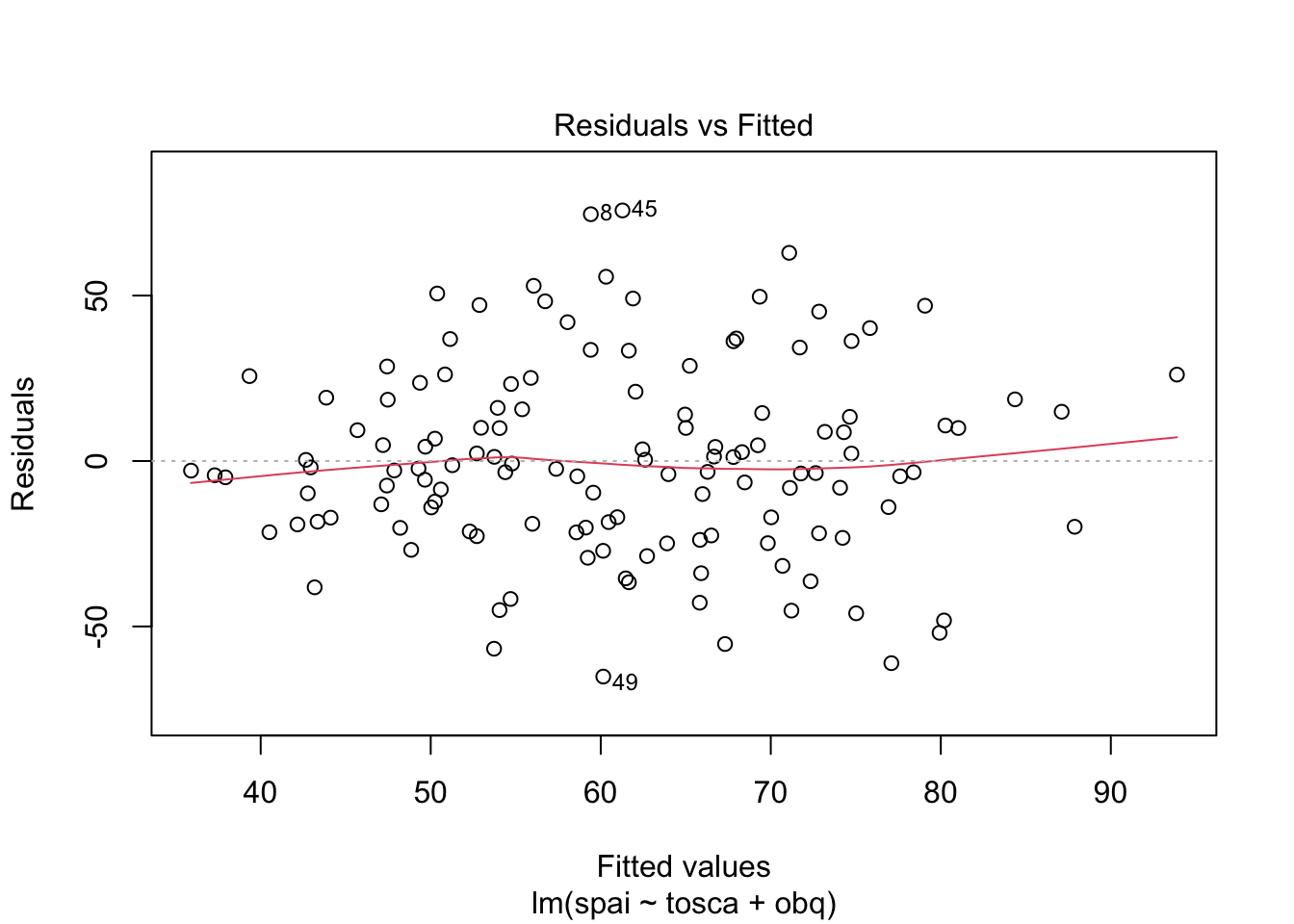
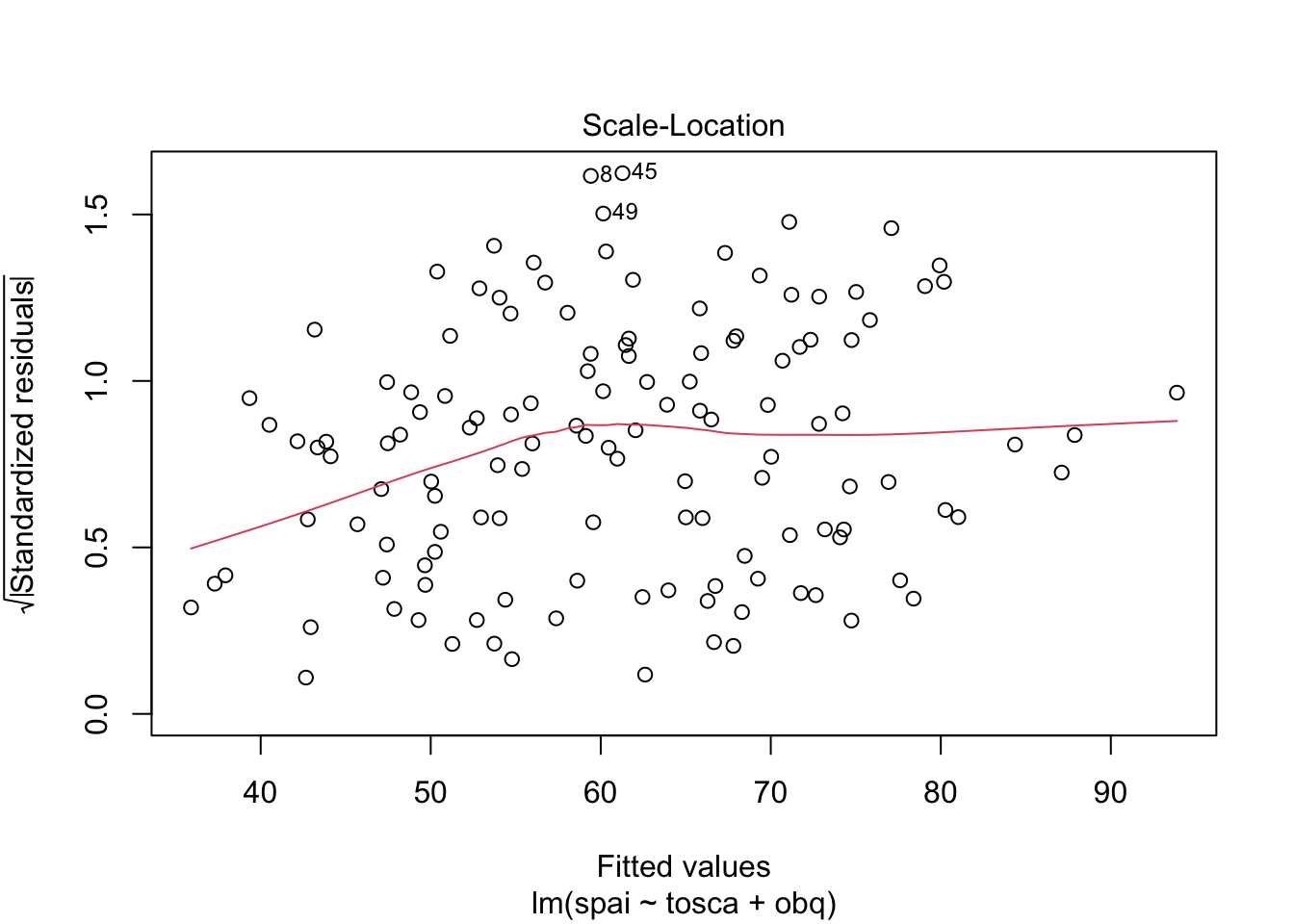
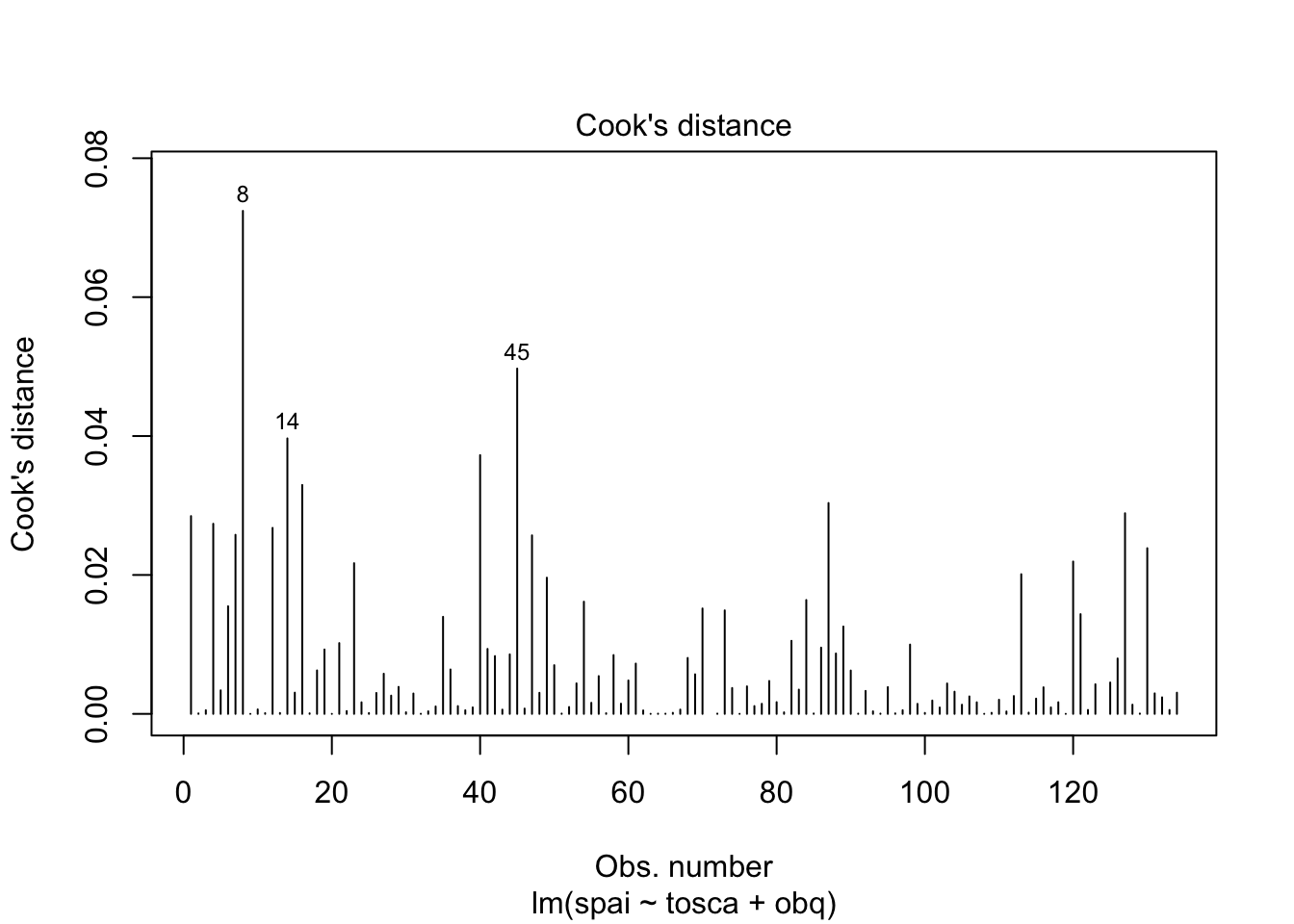
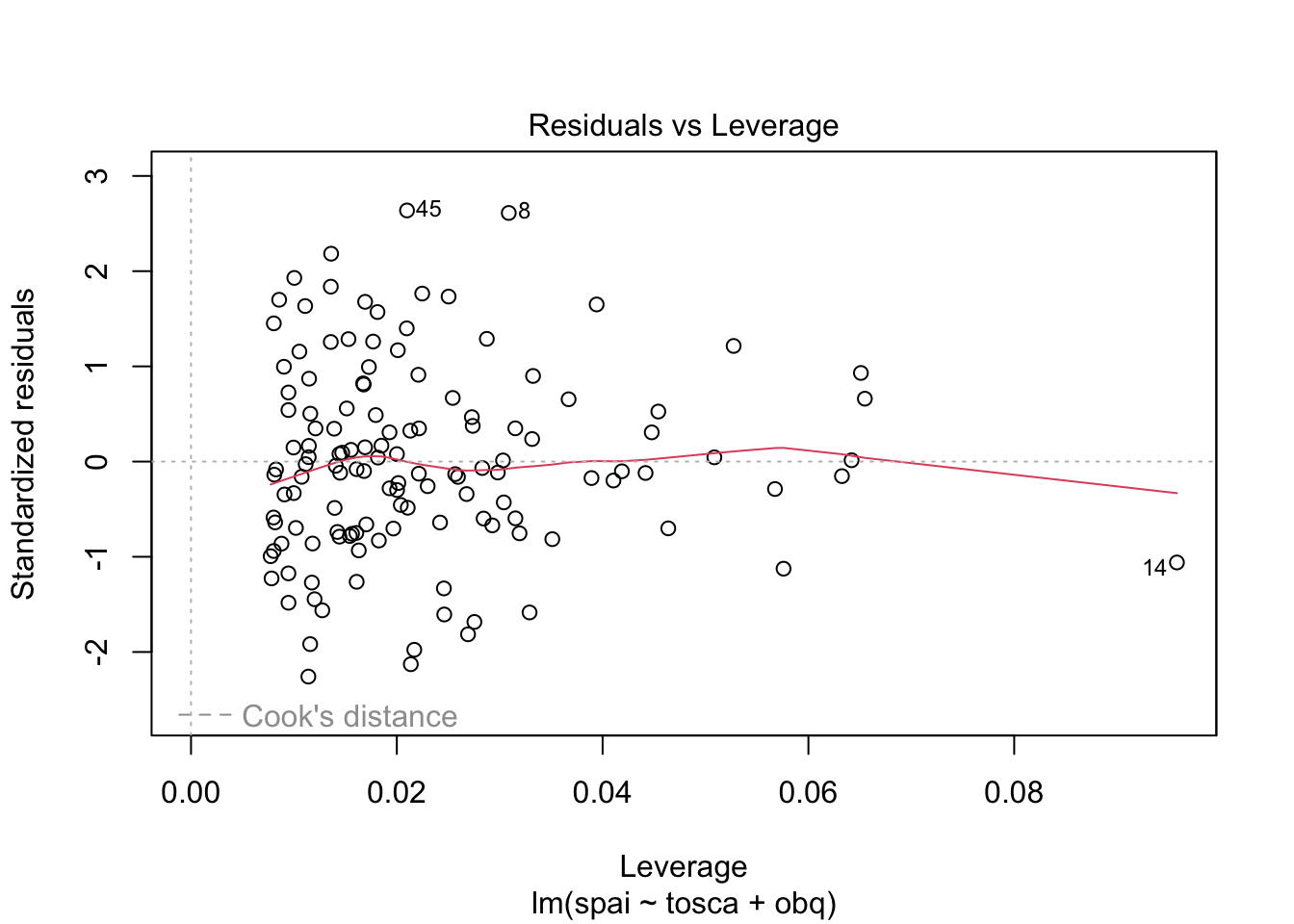
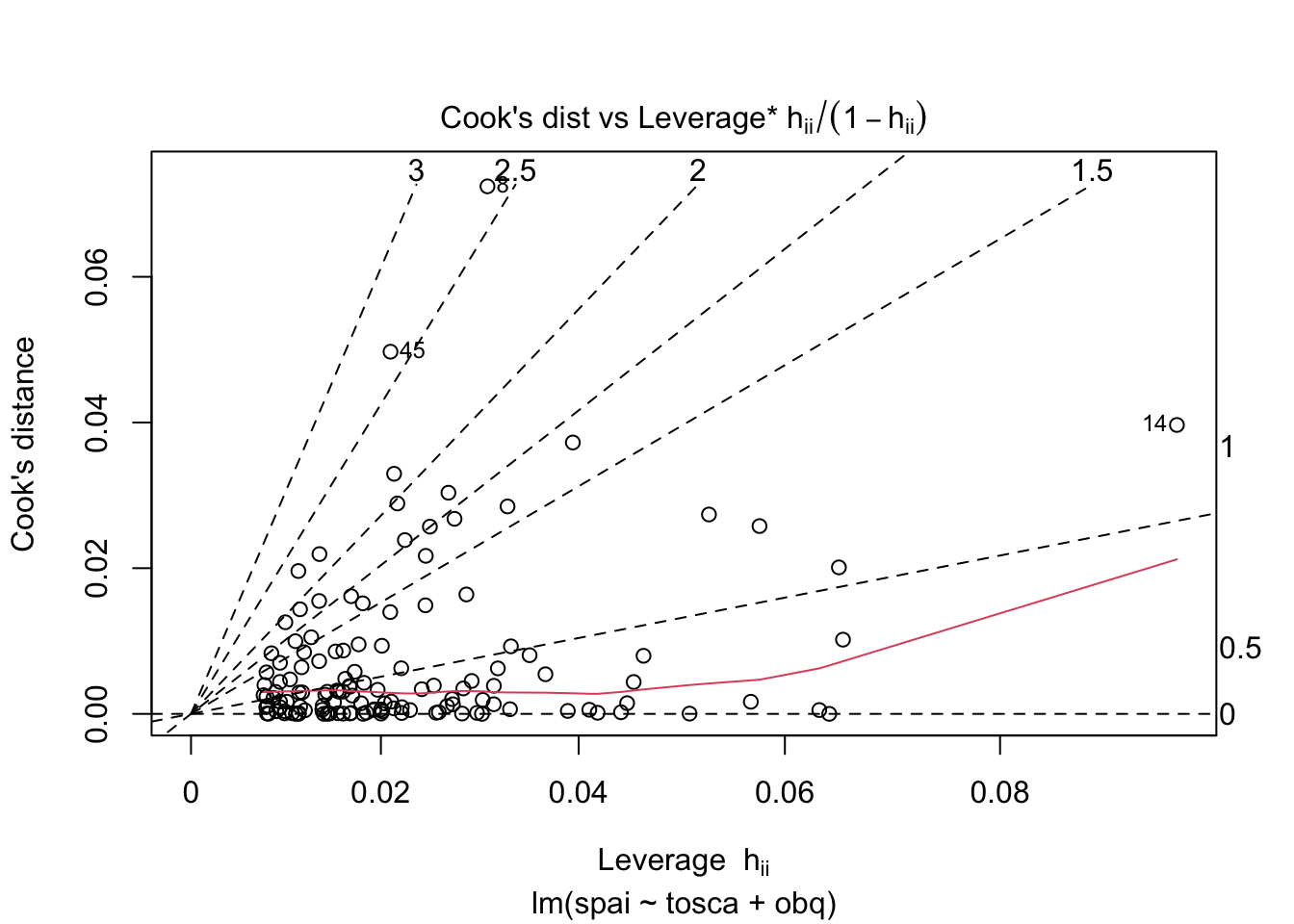
Warning: package 'ggplot2' was built under R version 4.5.2Warning: package 'tibble' was built under R version 4.5.2Warning: package 'tidyr' was built under R version 4.5.2Warning: package 'readr' was built under R version 4.5.2Warning: package 'purrr' was built under R version 4.5.2Warning: package 'dplyr' was built under R version 4.5.2── Attaching core tidyverse packages ──────────────────────── tidyverse 2.0.0 ──
✔ dplyr 1.2.0 ✔ readr 2.1.6
✔ forcats 1.0.1 ✔ stringr 1.6.0
✔ ggplot2 4.0.2 ✔ tibble 3.3.1
✔ lubridate 1.9.4 ✔ tidyr 1.3.2
✔ purrr 1.2.1
── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
✖ dplyr::filter() masks stats::filter()
✖ dplyr::lag() masks stats::lag()
ℹ Use the conflicted package (<http://conflicted.r-lib.org/>) to force all conflicts to become errorsLoading required package: fit.modelsRows: 200 Columns: 5
── Column specification ────────────────────────────────────────────────────────
Delimiter: ","
chr (1): album_id
dbl (4): adverts, sales, airplay, image
ℹ Use `spec()` to retrieve the full column specification for this data.
ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.Rows: 134 Columns: 4
── Column specification ────────────────────────────────────────────────────────
Delimiter: ","
dbl (4): spai, iii, obq, tosca
ℹ Use `spec()` to retrieve the full column specification for this data.
ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.Rows: 2506 Columns: 2
── Column specification ────────────────────────────────────────────────────────
Delimiter: ","
dbl (2): hm, suicide
ℹ Use `spec()` to retrieve the full column specification for this data.
ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.