dsus_18 - Exploratory Factor Analysis

library(tidyverse, knitr)

── Attaching core tidyverse packages ──────────────────────── tidyverse 2.0.0 ──
✔ dplyr     1.1.4     ✔ readr     2.1.5
✔ forcats   1.0.0     ✔ stringr   1.5.1
✔ ggplot2   3.5.1     ✔ tibble    3.2.1
✔ lubridate 1.9.3     ✔ tidyr     1.3.1
✔ purrr     1.0.2     
── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
✖ dplyr::filter() masks stats::filter()
✖ dplyr::lag()    masks stats::lag()
ℹ Use the conflicted package (<http://conflicted.r-lib.org/>) to force all conflicts to become errors

library(ggplot2, ggfortify, robust)
library(viridis)

Loading required package: viridisLite

library(GPArotation)

raq_tib <- here::here("data/raq.csv") |>
  readr::read_csv()

Rows: 2571 Columns: 24
── Column specification ────────────────────────────────────────────────────────
Delimiter: ","
chr  (1): id
dbl (23): raq_01, raq_02, raq_03, raq_04, raq_05, raq_06, raq_07, raq_08, ra...

ℹ Use `spec()` to retrieve the full column specification for this data.
ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.

Notes here are from

Field, A. P. (2018). Discovering statistics using IBM SPSS statistics (5th edition, North American edition). Sage Publications Inc. -> DSuS

Code examples will be from:

Field, A. (2023). discovr: Interactive tutorials and data for “Discovering Statistics Using R and RStudio” [Manual]. -> discovr

R Core Team. (2023). R: A language and environment for statistical computing [Manual]. R Foundation for Statistical Computing. https://www.R-project.org/

When to use factor analysis (p. 571)

• when attempting to measure latent variables
• factor analysis and principal component analysis are used to identify clusters of variables
• 3 main uses
  • understand the structure of a set of variables
  • to construct a questionnaire to measure an underlying variable
  • reduce the size of a data set while retaining as much of the original information as possible
    • (FA can be used to solve the problem of multicollinearity by combining factors that are collinear)

multicollinearity

exists when there is a strong correlation between two factors

multicollinearity makes it difficult or impossible to determine the amount of variance accounted for by one of two correlated factors

e.g., if a factor predicts the outcome variable with \(R=0.80\) and a second variable accounts for the same variance (i.e., it is highly correlated to the first variable) then it is only contributing to a very small amount of the unique variance in outcome and we might see \(R=0.82\). If the two predictor variables are uncorrelated, then the second variable is contributing more unique variance and we might see \(R=0.95\)

multicollinearity leads to interchangable predictors

Examples of factor analysis

• extroversion, introversion, neuroticism traits
• personality questionnaires
• in economics to see whether productivity, profits, and workforce contribute to the underlying dimension of company growth

EFA and PCA

• they are not the same thing
• but they both are used to reduce a set of variables into a smaller set of dimensions (factors in EFA, and components in PCA)

Factors and Components

• measuring several variables with several questions gives us data that can be arranged in a correlation matrix (R matrix) as below.

  Note: Created with the ggplot2 R package (Wickham 2016) with data from the discovr package (Field 2023.)

• factor analysis tries to explain the maximum amount of common variance in the matrix using the least number of explanatory constructs (latent variables), which represent clusters of variables that correlate highly with each other.

• PCA differs in that it tries to explain the maximum amount of total variance in a correlation matrix by transforming the original variables into linear components

Example - Induced Anxiety (discovr_18 Field (2023))

• questionnaire developed to measure anxiety related to using R
• questions developed from interviews with anxious and non-anxious students
• 23 questions; 5-point likert (strongly disagree -> strongly agree)
  • raq_01: Statistics make me cry
  • raq_02: My friends will think I’m stupid for not being able to cope with R
  • raq_03: Standard deviations excite me
  • raq_04: I dream that Pearson is attacking me with correlation coefficients
  • raq_05: I don’t understand statistics
  • raq_06: I have little experience of computers
  • raq_07: All computers hate me
  • raq_08: I have never been good at mathematics
  • raq_09: My friends are better at statistics than me
  • raq_10: Computers are useful only for playing games
  • raq_11: I did badly at mathematics at school
  • raq_12: People try to tell you that R makes statistics easier to understand but it doesn’t
  • raq_13: I worry that I will cause irreparable damage because of my incompetence with computers
  • raq_14: Computers have minds of their own and deliberately go wrong whenever I use them
  • raq_15: Computers are out to get me
  • raq_16: I weep openly at the mention of central tendency
  • raq_17: I slip into a coma whenever I see an equation
  • raq_18: R always crashes when I try to use it
  • raq_19: Everybody looks at me when I use R
  • raq_20: I can’t sleep for thoughts of eigenvectors
  • raq_21: I wake up under my duvet thinking that I am trapped under a normal distribution
  • raq_22: My friends are better at R than I am
  • raq_23: If I am good at statistics people will think I am a nerd

raq_tib

# A tibble: 2,571 × 24
   id    raq_01 raq_02 raq_03 raq_04 raq_05 raq_06 raq_07 raq_08 raq_09 raq_10
   <chr>  <dbl>  <dbl>  <dbl>  <dbl>  <dbl>  <dbl>  <dbl>  <dbl>  <dbl>  <dbl>
 1 157lk      3      1      3      4      2      4      3      3      3      2
 2 k3xjh      2      5      3      3      4      4      5      4      4      3
 3 832x6      4      5      3      3      3      4      5      4      3      4
 4 6dyt5      4      4      4      3      4      4      4      3      2      2
 5 w4upu      4      2      5      4      2      3      2      5      4      5
 6 9432i      2      3      4      3      4      2      3      2      3      2
 7 x03sh      2      4      5      5      3      3      4      3      3      3
 8 12v15      4      3      4      3      5      4      5      4      3      5
 9 46y22      3      5      5      1      3      4      4      3      5      3
10 1iqc4      2      5      3      2      4      5      5      5      4      4
# ℹ 2,561 more rows
# ℹ 13 more variables: raq_11 <dbl>, raq_12 <dbl>, raq_13 <dbl>, raq_14 <dbl>,
#   raq_15 <dbl>, raq_16 <dbl>, raq_17 <dbl>, raq_18 <dbl>, raq_19 <dbl>,
#   raq_20 <dbl>, raq_21 <dbl>, raq_22 <dbl>, raq_23 <dbl>

• 24 variables including the ID
• we don’t need the id in analyses so create a new tib without it

raq_items_tib <- raq_tib |> 
  dplyr::select(-id)
raq_items_tib

# A tibble: 2,571 × 23
   raq_01 raq_02 raq_03 raq_04 raq_05 raq_06 raq_07 raq_08 raq_09 raq_10 raq_11
    <dbl>  <dbl>  <dbl>  <dbl>  <dbl>  <dbl>  <dbl>  <dbl>  <dbl>  <dbl>  <dbl>
 1      3      1      3      4      2      4      3      3      3      2      2
 2      2      5      3      3      4      4      5      4      4      3      4
 3      4      5      3      3      3      4      5      4      3      4      4
 4      4      4      4      3      4      4      4      3      2      2      2
 5      4      2      5      4      2      3      2      5      4      5      4
 6      2      3      4      3      4      2      3      2      3      2      1
 7      2      4      5      5      3      3      4      3      3      3      3
 8      4      3      4      3      5      4      5      4      3      5      3
 9      3      5      5      1      3      4      4      3      5      3      3
10      2      5      3      2      4      5      5      5      4      4      4
# ℹ 2,561 more rows
# ℹ 12 more variables: raq_12 <dbl>, raq_13 <dbl>, raq_14 <dbl>, raq_15 <dbl>,
#   raq_16 <dbl>, raq_17 <dbl>, raq_18 <dbl>, raq_19 <dbl>, raq_20 <dbl>,
#   raq_21 <dbl>, raq_22 <dbl>, raq_23 <dbl>

Correlation matrix

# feed the tibble with only the RAQ items into the correlation() function
correlation::correlation(raq_items_tib)

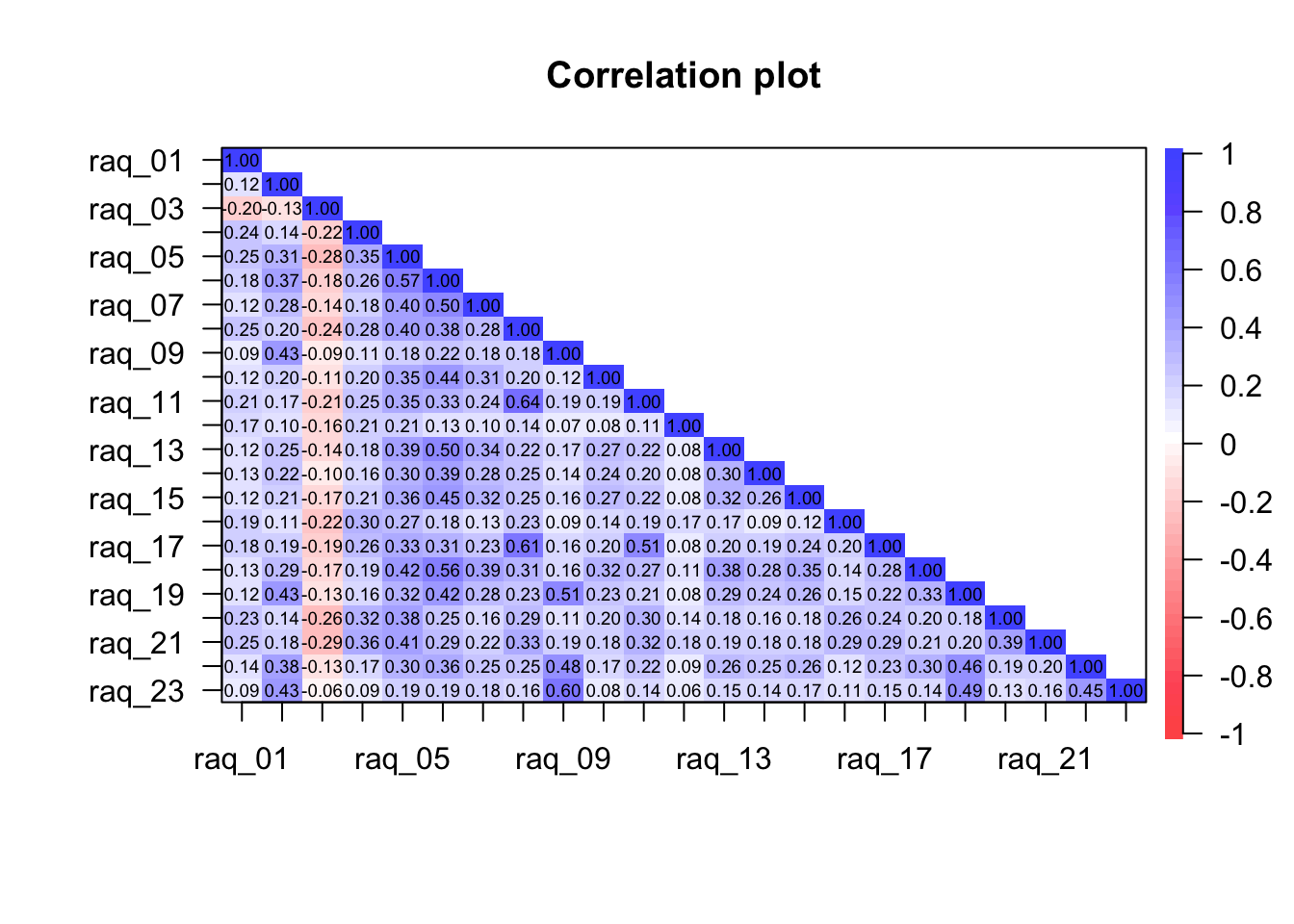
# Correlation Matrix (pearson-method)

Parameter1 | Parameter2 |     r |         95% CI | t(2569) |         p
----------------------------------------------------------------------
raq_01     |     raq_02 |  0.11 | [ 0.07,  0.15] |    5.47 | < .001***
raq_01     |     raq_03 | -0.18 | [-0.22, -0.14] |   -9.21 | < .001***
raq_01     |     raq_04 |  0.22 | [ 0.18,  0.25] |   11.26 | < .001***
raq_01     |     raq_05 |  0.22 | [ 0.19,  0.26] |   11.60 | < .001***
raq_01     |     raq_06 |  0.16 | [ 0.12,  0.20] |    8.17 | < .001***
raq_01     |     raq_07 |  0.11 | [ 0.07,  0.14] |    5.41 | < .001***
raq_01     |     raq_08 |  0.22 | [ 0.18,  0.26] |   11.53 | < .001***
raq_01     |     raq_09 |  0.08 | [ 0.05,  0.12] |    4.26 | < .001***
raq_01     |     raq_10 |  0.11 | [ 0.07,  0.15] |    5.70 | < .001***
raq_01     |     raq_11 |  0.19 | [ 0.15,  0.23] |    9.76 | < .001***
raq_01     |     raq_12 |  0.15 | [ 0.11,  0.19] |    7.67 | < .001***
raq_01     |     raq_13 |  0.11 | [ 0.07,  0.15] |    5.55 | < .001***
raq_01     |     raq_14 |  0.12 | [ 0.08,  0.15] |    5.87 | < .001***
raq_01     |     raq_15 |  0.11 | [ 0.07,  0.15] |    5.61 | < .001***
raq_01     |     raq_16 |  0.18 | [ 0.14,  0.21] |    9.04 | < .001***
raq_01     |     raq_17 |  0.17 | [ 0.13,  0.20] |    8.52 | < .001***
raq_01     |     raq_18 |  0.12 | [ 0.08,  0.16] |    6.06 | < .001***
raq_01     |     raq_19 |  0.11 | [ 0.07,  0.14] |    5.45 | < .001***
raq_01     |     raq_20 |  0.21 | [ 0.17,  0.24] |   10.73 | < .001***
raq_01     |     raq_21 |  0.23 | [ 0.19,  0.26] |   11.81 | < .001***
raq_01     |     raq_22 |  0.12 | [ 0.09,  0.16] |    6.30 | < .001***
raq_01     |     raq_23 |  0.08 | [ 0.04,  0.12] |    3.93 | < .001***
raq_02     |     raq_03 | -0.12 | [-0.16, -0.08] |   -6.14 | < .001***
raq_02     |     raq_04 |  0.12 | [ 0.09,  0.16] |    6.31 | < .001***
raq_02     |     raq_05 |  0.28 | [ 0.24,  0.31] |   14.71 | < .001***
raq_02     |     raq_06 |  0.34 | [ 0.30,  0.37] |   18.19 | < .001***
raq_02     |     raq_07 |  0.26 | [ 0.22,  0.29] |   13.44 | < .001***
raq_02     |     raq_08 |  0.18 | [ 0.14,  0.22] |    9.16 | < .001***
raq_02     |     raq_09 |  0.39 | [ 0.36,  0.42] |   21.50 | < .001***
raq_02     |     raq_10 |  0.18 | [ 0.15,  0.22] |    9.48 | < .001***
raq_02     |     raq_11 |  0.15 | [ 0.11,  0.19] |    7.82 | < .001***
raq_02     |     raq_12 |  0.09 | [ 0.05,  0.13] |    4.58 | < .001***
raq_02     |     raq_13 |  0.23 | [ 0.19,  0.27] |   11.96 | < .001***
raq_02     |     raq_14 |  0.20 | [ 0.16,  0.23] |   10.21 | < .001***
raq_02     |     raq_15 |  0.19 | [ 0.15,  0.22] |    9.64 | < .001***
raq_02     |     raq_16 |  0.10 | [ 0.06,  0.13] |    4.92 | < .001***
raq_02     |     raq_17 |  0.17 | [ 0.14,  0.21] |    8.94 | < .001***
raq_02     |     raq_18 |  0.26 | [ 0.23,  0.30] |   13.87 | < .001***
raq_02     |     raq_19 |  0.39 | [ 0.36,  0.42] |   21.50 | < .001***
raq_02     |     raq_20 |  0.13 | [ 0.09,  0.17] |    6.55 | < .001***
raq_02     |     raq_21 |  0.16 | [ 0.12,  0.20] |    8.26 | < .001***
raq_02     |     raq_22 |  0.34 | [ 0.30,  0.37] |   18.28 | < .001***
raq_02     |     raq_23 |  0.39 | [ 0.36,  0.42] |   21.56 | < .001***
raq_03     |     raq_04 | -0.19 | [-0.23, -0.16] |  -10.01 | < .001***
raq_03     |     raq_05 | -0.25 | [-0.29, -0.22] |  -13.34 | < .001***
raq_03     |     raq_06 | -0.17 | [-0.20, -0.13] |   -8.51 | < .001***
raq_03     |     raq_07 | -0.13 | [-0.16, -0.09] |   -6.45 | < .001***
raq_03     |     raq_08 | -0.22 | [-0.25, -0.18] |  -11.33 | < .001***
raq_03     |     raq_09 | -0.08 | [-0.12, -0.04] |   -4.14 | < .001***
raq_03     |     raq_10 | -0.10 | [-0.14, -0.06] |   -5.18 | < .001***
raq_03     |     raq_11 | -0.19 | [-0.23, -0.15] |   -9.81 | < .001***
raq_03     |     raq_12 | -0.15 | [-0.19, -0.11] |   -7.58 | < .001***
raq_03     |     raq_13 | -0.13 | [-0.17, -0.09] |   -6.71 | < .001***
raq_03     |     raq_14 | -0.09 | [-0.13, -0.05] |   -4.45 | < .001***
raq_03     |     raq_15 | -0.15 | [-0.19, -0.11] |   -7.57 | < .001***
raq_03     |     raq_16 | -0.20 | [-0.24, -0.17] |  -10.56 | < .001***
raq_03     |     raq_17 | -0.18 | [-0.21, -0.14] |   -9.01 | < .001***
raq_03     |     raq_18 | -0.15 | [-0.19, -0.11] |   -7.78 | < .001***
raq_03     |     raq_19 | -0.12 | [-0.15, -0.08] |   -5.96 | < .001***
raq_03     |     raq_20 | -0.23 | [-0.27, -0.20] |  -12.20 | < .001***
raq_03     |     raq_21 | -0.26 | [-0.30, -0.22] |  -13.62 | < .001***
raq_03     |     raq_22 | -0.12 | [-0.16, -0.08] |   -6.00 | < .001***
raq_03     |     raq_23 | -0.05 | [-0.09, -0.01] |   -2.65 | 0.014*   
raq_04     |     raq_05 |  0.32 | [ 0.28,  0.35] |   17.08 | < .001***
raq_04     |     raq_06 |  0.23 | [ 0.20,  0.27] |   12.21 | < .001***
raq_04     |     raq_07 |  0.17 | [ 0.13,  0.20] |    8.56 | < .001***
raq_04     |     raq_08 |  0.25 | [ 0.21,  0.28] |   12.96 | < .001***
raq_04     |     raq_09 |  0.10 | [ 0.06,  0.14] |    4.98 | < .001***
raq_04     |     raq_10 |  0.18 | [ 0.14,  0.21] |    9.11 | < .001***
raq_04     |     raq_11 |  0.22 | [ 0.18,  0.26] |   11.54 | < .001***
raq_04     |     raq_12 |  0.20 | [ 0.16,  0.23] |   10.12 | < .001***
raq_04     |     raq_13 |  0.16 | [ 0.13,  0.20] |    8.42 | < .001***
raq_04     |     raq_14 |  0.15 | [ 0.11,  0.18] |    7.55 | < .001***
raq_04     |     raq_15 |  0.18 | [ 0.15,  0.22] |    9.50 | < .001***
raq_04     |     raq_16 |  0.27 | [ 0.23,  0.31] |   14.25 | < .001***
raq_04     |     raq_17 |  0.24 | [ 0.20,  0.27] |   12.36 | < .001***
raq_04     |     raq_18 |  0.17 | [ 0.13,  0.21] |    8.81 | < .001***
raq_04     |     raq_19 |  0.14 | [ 0.10,  0.18] |    7.24 | < .001***
raq_04     |     raq_20 |  0.28 | [ 0.25,  0.32] |   15.00 | < .001***
raq_04     |     raq_21 |  0.32 | [ 0.28,  0.35] |   17.12 | < .001***
raq_04     |     raq_22 |  0.16 | [ 0.12,  0.19] |    8.07 | < .001***
raq_04     |     raq_23 |  0.08 | [ 0.04,  0.12] |    4.22 | < .001***
raq_05     |     raq_06 |  0.51 | [ 0.48,  0.54] |   30.26 | < .001***
raq_05     |     raq_07 |  0.36 | [ 0.33,  0.40] |   19.79 | < .001***
raq_05     |     raq_08 |  0.36 | [ 0.32,  0.39] |   19.39 | < .001***
raq_05     |     raq_09 |  0.16 | [ 0.12,  0.20] |    8.28 | < .001***
raq_05     |     raq_10 |  0.31 | [ 0.28,  0.35] |   16.67 | < .001***
raq_05     |     raq_11 |  0.31 | [ 0.28,  0.35] |   16.61 | < .001***
raq_05     |     raq_12 |  0.19 | [ 0.15,  0.22] |    9.66 | < .001***
raq_05     |     raq_13 |  0.35 | [ 0.32,  0.38] |   19.00 | < .001***
raq_05     |     raq_14 |  0.27 | [ 0.23,  0.30] |   14.05 | < .001***
raq_05     |     raq_15 |  0.33 | [ 0.29,  0.36] |   17.54 | < .001***
raq_05     |     raq_16 |  0.24 | [ 0.20,  0.28] |   12.53 | < .001***
raq_05     |     raq_17 |  0.30 | [ 0.27,  0.34] |   16.01 | < .001***
raq_05     |     raq_18 |  0.38 | [ 0.35,  0.41] |   20.97 | < .001***
raq_05     |     raq_19 |  0.29 | [ 0.26,  0.33] |   15.50 | < .001***
raq_05     |     raq_20 |  0.34 | [ 0.31,  0.37] |   18.36 | < .001***
raq_05     |     raq_21 |  0.37 | [ 0.34,  0.40] |   20.24 | < .001***
raq_05     |     raq_22 |  0.27 | [ 0.23,  0.31] |   14.26 | < .001***
raq_05     |     raq_23 |  0.17 | [ 0.13,  0.21] |    8.70 | < .001***
raq_06     |     raq_07 |  0.45 | [ 0.42,  0.48] |   25.68 | < .001***
raq_06     |     raq_08 |  0.34 | [ 0.31,  0.37] |   18.36 | < .001***
raq_06     |     raq_09 |  0.20 | [ 0.16,  0.24] |   10.40 | < .001***
raq_06     |     raq_10 |  0.40 | [ 0.36,  0.43] |   21.93 | < .001***
raq_06     |     raq_11 |  0.29 | [ 0.26,  0.33] |   15.55 | < .001***
raq_06     |     raq_12 |  0.11 | [ 0.07,  0.15] |    5.74 | < .001***
raq_06     |     raq_13 |  0.46 | [ 0.42,  0.49] |   25.90 | < .001***
raq_06     |     raq_14 |  0.36 | [ 0.32,  0.39] |   19.25 | < .001***
raq_06     |     raq_15 |  0.40 | [ 0.37,  0.43] |   22.20 | < .001***
raq_06     |     raq_16 |  0.16 | [ 0.12,  0.20] |    8.21 | < .001***
raq_06     |     raq_17 |  0.28 | [ 0.24,  0.32] |   14.83 | < .001***
raq_06     |     raq_18 |  0.51 | [ 0.48,  0.54] |   30.01 | < .001***
raq_06     |     raq_19 |  0.38 | [ 0.34,  0.41] |   20.64 | < .001***
raq_06     |     raq_20 |  0.23 | [ 0.19,  0.26] |   11.74 | < .001***
raq_06     |     raq_21 |  0.26 | [ 0.23,  0.30] |   13.86 | < .001***
raq_06     |     raq_22 |  0.33 | [ 0.29,  0.36] |   17.48 | < .001***
raq_06     |     raq_23 |  0.17 | [ 0.13,  0.21] |    8.85 | < .001***
raq_07     |     raq_08 |  0.25 | [ 0.21,  0.28] |   13.03 | < .001***
raq_07     |     raq_09 |  0.17 | [ 0.13,  0.20] |    8.48 | < .001***
raq_07     |     raq_10 |  0.28 | [ 0.25,  0.32] |   14.94 | < .001***
raq_07     |     raq_11 |  0.21 | [ 0.18,  0.25] |   11.02 | < .001***
raq_07     |     raq_12 |  0.10 | [ 0.06,  0.13] |    4.89 | < .001***
raq_07     |     raq_13 |  0.31 | [ 0.28,  0.35] |   16.58 | < .001***
raq_07     |     raq_14 |  0.25 | [ 0.21,  0.29] |   13.16 | < .001***
raq_07     |     raq_15 |  0.29 | [ 0.25,  0.32] |   15.28 | < .001***
raq_07     |     raq_16 |  0.12 | [ 0.08,  0.16] |    6.21 | < .001***
raq_07     |     raq_17 |  0.21 | [ 0.17,  0.25] |   10.94 | < .001***
raq_07     |     raq_18 |  0.35 | [ 0.32,  0.38] |   18.93 | < .001***
raq_07     |     raq_19 |  0.26 | [ 0.22,  0.29] |   13.41 | < .001***
raq_07     |     raq_20 |  0.14 | [ 0.10,  0.18] |    7.17 | < .001***
raq_07     |     raq_21 |  0.20 | [ 0.16,  0.23] |   10.19 | < .001***
raq_07     |     raq_22 |  0.22 | [ 0.19,  0.26] |   11.69 | < .001***
raq_07     |     raq_23 |  0.16 | [ 0.12,  0.20] |    8.24 | < .001***
raq_08     |     raq_09 |  0.16 | [ 0.13,  0.20] |    8.45 | < .001***
raq_08     |     raq_10 |  0.19 | [ 0.15,  0.22] |    9.58 | < .001***
raq_08     |     raq_11 |  0.58 | [ 0.56,  0.61] |   36.28 | < .001***
raq_08     |     raq_12 |  0.13 | [ 0.09,  0.17] |    6.58 | < .001***
raq_08     |     raq_13 |  0.20 | [ 0.16,  0.24] |   10.38 | < .001***
raq_08     |     raq_14 |  0.23 | [ 0.19,  0.27] |   12.01 | < .001***
raq_08     |     raq_15 |  0.23 | [ 0.19,  0.27] |   11.97 | < .001***
raq_08     |     raq_16 |  0.21 | [ 0.17,  0.24] |   10.69 | < .001***
raq_08     |     raq_17 |  0.55 | [ 0.52,  0.57] |   33.20 | < .001***
raq_08     |     raq_18 |  0.28 | [ 0.24,  0.31] |   14.68 | < .001***
raq_08     |     raq_19 |  0.21 | [ 0.17,  0.25] |   10.86 | < .001***
raq_08     |     raq_20 |  0.26 | [ 0.23,  0.30] |   13.76 | < .001***
raq_08     |     raq_21 |  0.30 | [ 0.27,  0.34] |   16.15 | < .001***
raq_08     |     raq_22 |  0.22 | [ 0.19,  0.26] |   11.68 | < .001***
raq_08     |     raq_23 |  0.14 | [ 0.10,  0.18] |    7.25 | < .001***
raq_09     |     raq_10 |  0.11 | [ 0.07,  0.14] |    5.38 | < .001***
raq_09     |     raq_11 |  0.17 | [ 0.14,  0.21] |    9.01 | < .001***
raq_09     |     raq_12 |  0.06 | [ 0.02,  0.10] |    3.07 | 0.007**  
raq_09     |     raq_13 |  0.15 | [ 0.11,  0.19] |    7.84 | < .001***
raq_09     |     raq_14 |  0.12 | [ 0.09,  0.16] |    6.30 | < .001***
raq_09     |     raq_15 |  0.15 | [ 0.11,  0.19] |    7.60 | < .001***
raq_09     |     raq_16 |  0.08 | [ 0.04,  0.12] |    4.19 | < .001***
raq_09     |     raq_17 |  0.14 | [ 0.10,  0.18] |    7.32 | < .001***
raq_09     |     raq_18 |  0.15 | [ 0.11,  0.18] |    7.52 | < .001***
raq_09     |     raq_19 |  0.46 | [ 0.43,  0.49] |   26.59 | < .001***
raq_09     |     raq_20 |  0.10 | [ 0.06,  0.14] |    5.08 | < .001***
raq_09     |     raq_21 |  0.17 | [ 0.13,  0.20] |    8.61 | < .001***
raq_09     |     raq_22 |  0.43 | [ 0.40,  0.46] |   23.95 | < .001***
raq_09     |     raq_23 |  0.55 | [ 0.52,  0.57] |   33.09 | < .001***
raq_10     |     raq_11 |  0.17 | [ 0.13,  0.21] |    8.68 | < .001***
raq_10     |     raq_12 |  0.08 | [ 0.04,  0.11] |    3.85 | 0.001**  
raq_10     |     raq_13 |  0.25 | [ 0.21,  0.28] |   12.99 | < .001***
raq_10     |     raq_14 |  0.22 | [ 0.18,  0.26] |   11.38 | < .001***
raq_10     |     raq_15 |  0.24 | [ 0.21,  0.28] |   12.68 | < .001***
raq_10     |     raq_16 |  0.13 | [ 0.09,  0.17] |    6.59 | < .001***
raq_10     |     raq_17 |  0.18 | [ 0.14,  0.21] |    9.12 | < .001***
raq_10     |     raq_18 |  0.29 | [ 0.26,  0.33] |   15.43 | < .001***
raq_10     |     raq_19 |  0.21 | [ 0.17,  0.25] |   10.97 | < .001***
raq_10     |     raq_20 |  0.18 | [ 0.14,  0.22] |    9.23 | < .001***
raq_10     |     raq_21 |  0.16 | [ 0.12,  0.20] |    8.34 | < .001***
raq_10     |     raq_22 |  0.16 | [ 0.12,  0.19] |    7.98 | < .001***
raq_10     |     raq_23 |  0.07 | [ 0.03,  0.11] |    3.53 | 0.003**  
raq_11     |     raq_12 |  0.10 | [ 0.07,  0.14] |    5.27 | < .001***
raq_11     |     raq_13 |  0.20 | [ 0.16,  0.24] |   10.40 | < .001***
raq_11     |     raq_14 |  0.19 | [ 0.15,  0.22] |    9.59 | < .001***
raq_11     |     raq_15 |  0.20 | [ 0.16,  0.24] |   10.42 | < .001***
raq_11     |     raq_16 |  0.17 | [ 0.14,  0.21] |    9.00 | < .001***
raq_11     |     raq_17 |  0.47 | [ 0.43,  0.49] |   26.63 | < .001***
raq_11     |     raq_18 |  0.24 | [ 0.20,  0.28] |   12.48 | < .001***
raq_11     |     raq_19 |  0.19 | [ 0.16,  0.23] |   10.04 | < .001***
raq_11     |     raq_20 |  0.27 | [ 0.23,  0.31] |   14.19 | < .001***
raq_11     |     raq_21 |  0.29 | [ 0.25,  0.32] |   15.15 | < .001***
raq_11     |     raq_22 |  0.20 | [ 0.16,  0.24] |   10.44 | < .001***
raq_11     |     raq_23 |  0.13 | [ 0.09,  0.17] |    6.56 | < .001***
raq_12     |     raq_13 |  0.07 | [ 0.03,  0.11] |    3.48 | 0.003**  
raq_12     |     raq_14 |  0.07 | [ 0.03,  0.11] |    3.50 | 0.003**  
raq_12     |     raq_15 |  0.07 | [ 0.03,  0.11] |    3.63 | 0.002**  
raq_12     |     raq_16 |  0.15 | [ 0.12,  0.19] |    7.87 | < .001***
raq_12     |     raq_17 |  0.07 | [ 0.03,  0.11] |    3.71 | 0.002**  
raq_12     |     raq_18 |  0.10 | [ 0.06,  0.14] |    5.00 | < .001***
raq_12     |     raq_19 |  0.07 | [ 0.03,  0.11] |    3.40 | 0.003**  
raq_12     |     raq_20 |  0.12 | [ 0.08,  0.16] |    6.27 | < .001***
raq_12     |     raq_21 |  0.16 | [ 0.13,  0.20] |    8.42 | < .001***
raq_12     |     raq_22 |  0.08 | [ 0.04,  0.12] |    4.05 | < .001***
raq_12     |     raq_23 |  0.05 | [ 0.01,  0.09] |    2.70 | 0.014*   
raq_13     |     raq_14 |  0.27 | [ 0.24,  0.31] |   14.44 | < .001***
raq_13     |     raq_15 |  0.29 | [ 0.25,  0.32] |   15.31 | < .001***
raq_13     |     raq_16 |  0.15 | [ 0.11,  0.19] |    7.66 | < .001***
raq_13     |     raq_17 |  0.18 | [ 0.14,  0.21] |    9.12 | < .001***
raq_13     |     raq_18 |  0.34 | [ 0.31,  0.37] |   18.35 | < .001***
raq_13     |     raq_19 |  0.26 | [ 0.22,  0.30] |   13.64 | < .001***
raq_13     |     raq_20 |  0.16 | [ 0.12,  0.20] |    8.32 | < .001***
raq_13     |     raq_21 |  0.17 | [ 0.14,  0.21] |    8.98 | < .001***
raq_13     |     raq_22 |  0.23 | [ 0.19,  0.27] |   11.97 | < .001***
raq_13     |     raq_23 |  0.14 | [ 0.10,  0.18] |    7.15 | < .001***
raq_14     |     raq_15 |  0.23 | [ 0.20,  0.27] |   12.20 | < .001***
raq_14     |     raq_16 |  0.08 | [ 0.05,  0.12] |    4.29 | < .001***
raq_14     |     raq_17 |  0.17 | [ 0.13,  0.20] |    8.61 | < .001***
raq_14     |     raq_18 |  0.26 | [ 0.22,  0.29] |   13.40 | < .001***
raq_14     |     raq_19 |  0.22 | [ 0.18,  0.26] |   11.49 | < .001***
raq_14     |     raq_20 |  0.15 | [ 0.11,  0.19] |    7.60 | < .001***
raq_14     |     raq_21 |  0.17 | [ 0.13,  0.20] |    8.57 | < .001***
raq_14     |     raq_22 |  0.22 | [ 0.18,  0.26] |   11.43 | < .001***
raq_14     |     raq_23 |  0.13 | [ 0.09,  0.16] |    6.47 | < .001***
raq_15     |     raq_16 |  0.11 | [ 0.07,  0.15] |    5.59 | < .001***
raq_15     |     raq_17 |  0.21 | [ 0.18,  0.25] |   11.06 | < .001***
raq_15     |     raq_18 |  0.32 | [ 0.29,  0.35] |   17.13 | < .001***
raq_15     |     raq_19 |  0.23 | [ 0.19,  0.27] |   11.99 | < .001***
raq_15     |     raq_20 |  0.16 | [ 0.12,  0.20] |    8.12 | < .001***
raq_15     |     raq_21 |  0.17 | [ 0.13,  0.20] |    8.50 | < .001***
raq_15     |     raq_22 |  0.24 | [ 0.20,  0.27] |   12.38 | < .001***
raq_15     |     raq_23 |  0.15 | [ 0.11,  0.19] |    7.71 | < .001***
raq_16     |     raq_17 |  0.18 | [ 0.14,  0.21] |    9.10 | < .001***
raq_16     |     raq_18 |  0.12 | [ 0.09,  0.16] |    6.36 | < .001***
raq_16     |     raq_19 |  0.14 | [ 0.10,  0.17] |    6.93 | < .001***
raq_16     |     raq_20 |  0.23 | [ 0.20,  0.27] |   12.11 | < .001***
raq_16     |     raq_21 |  0.26 | [ 0.23,  0.30] |   13.87 | < .001***
raq_16     |     raq_22 |  0.11 | [ 0.07,  0.15] |    5.58 | < .001***
raq_16     |     raq_23 |  0.10 | [ 0.06,  0.14] |    5.10 | < .001***
raq_17     |     raq_18 |  0.25 | [ 0.22,  0.29] |   13.31 | < .001***
raq_17     |     raq_19 |  0.20 | [ 0.16,  0.23] |   10.17 | < .001***
raq_17     |     raq_20 |  0.22 | [ 0.18,  0.26] |   11.38 | < .001***
raq_17     |     raq_21 |  0.26 | [ 0.22,  0.29] |   13.54 | < .001***
raq_17     |     raq_22 |  0.21 | [ 0.17,  0.24] |   10.71 | < .001***
raq_17     |     raq_23 |  0.14 | [ 0.10,  0.17] |    7.01 | < .001***
raq_18     |     raq_19 |  0.30 | [ 0.26,  0.33] |   15.91 | < .001***
raq_18     |     raq_20 |  0.18 | [ 0.14,  0.22] |    9.24 | < .001***
raq_18     |     raq_21 |  0.19 | [ 0.16,  0.23] |    9.97 | < .001***
raq_18     |     raq_22 |  0.27 | [ 0.23,  0.30] |   14.08 | < .001***
raq_18     |     raq_23 |  0.13 | [ 0.09,  0.17] |    6.65 | < .001***
raq_19     |     raq_20 |  0.16 | [ 0.13,  0.20] |    8.43 | < .001***
raq_19     |     raq_21 |  0.18 | [ 0.15,  0.22] |    9.47 | < .001***
raq_19     |     raq_22 |  0.42 | [ 0.39,  0.45] |   23.34 | < .001***
raq_19     |     raq_23 |  0.44 | [ 0.41,  0.47] |   24.85 | < .001***
raq_20     |     raq_21 |  0.35 | [ 0.31,  0.38] |   18.85 | < .001***
raq_20     |     raq_22 |  0.17 | [ 0.13,  0.21] |    8.65 | < .001***
raq_20     |     raq_23 |  0.11 | [ 0.08,  0.15] |    5.82 | < .001***
raq_21     |     raq_22 |  0.18 | [ 0.14,  0.21] |    9.16 | < .001***
raq_21     |     raq_23 |  0.14 | [ 0.10,  0.18] |    7.28 | < .001***
raq_22     |     raq_23 |  0.40 | [ 0.37,  0.43] |   22.17 | < .001***

p-value adjustment method: Holm (1979)
Observations: 2571

# pipe into summary() to get a condensed table of correlations:
correlation::correlation(raq_items_tib) |>
  summary() |> 
  knitr::kable(digits = 2)

Parameter	raq_23	raq_22	raq_21	raq_20	raq_19	raq_18	raq_17	raq_16	raq_15	raq_14	raq_13	raq_12	raq_11	raq_10	raq_09	raq_08	raq_07	raq_06	raq_05	raq_04	raq_03	raq_02
raq_01	0.08	0.12	0.23	0.21	0.11	0.12	0.17	0.18	0.11	0.12	0.11	0.15	0.19	0.11	0.08	0.22	0.11	0.16	0.22	0.22	-0.18	0.11
raq_02	0.39	0.34	0.16	0.13	0.39	0.26	0.17	0.10	0.19	0.20	0.23	0.09	0.15	0.18	0.39	0.18	0.26	0.34	0.28	0.12	-0.12	NA
raq_03	-0.05	-0.12	-0.26	-0.23	-0.12	-0.15	-0.18	-0.20	-0.15	-0.09	-0.13	-0.15	-0.19	-0.10	-0.08	-0.22	-0.13	-0.17	-0.25	-0.19	NA	NA
raq_04	0.08	0.16	0.32	0.28	0.14	0.17	0.24	0.27	0.18	0.15	0.16	0.20	0.22	0.18	0.10	0.25	0.17	0.23	0.32	NA	NA	NA
raq_05	0.17	0.27	0.37	0.34	0.29	0.38	0.30	0.24	0.33	0.27	0.35	0.19	0.31	0.31	0.16	0.36	0.36	0.51	NA	NA	NA	NA
raq_06	0.17	0.33	0.26	0.23	0.38	0.51	0.28	0.16	0.40	0.36	0.46	0.11	0.29	0.40	0.20	0.34	0.45	NA	NA	NA	NA	NA
raq_07	0.16	0.22	0.20	0.14	0.26	0.35	0.21	0.12	0.29	0.25	0.31	0.10	0.21	0.28	0.17	0.25	NA	NA	NA	NA	NA	NA
raq_08	0.14	0.22	0.30	0.26	0.21	0.28	0.55	0.21	0.23	0.23	0.20	0.13	0.58	0.19	0.16	NA	NA	NA	NA	NA	NA	NA
raq_09	0.55	0.43	0.17	0.10	0.46	0.15	0.14	0.08	0.15	0.12	0.15	0.06	0.17	0.11	NA	NA	NA	NA	NA	NA	NA	NA
raq_10	0.07	0.16	0.16	0.18	0.21	0.29	0.18	0.13	0.24	0.22	0.25	0.08	0.17	NA	NA	NA	NA	NA	NA	NA	NA	NA
raq_11	0.13	0.20	0.29	0.27	0.19	0.24	0.47	0.17	0.20	0.19	0.20	0.10	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA
raq_12	0.05	0.08	0.16	0.12	0.07	0.10	0.07	0.15	0.07	0.07	0.07	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA
raq_13	0.14	0.23	0.17	0.16	0.26	0.34	0.18	0.15	0.29	0.27	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA
raq_14	0.13	0.22	0.17	0.15	0.22	0.26	0.17	0.08	0.23	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA
raq_15	0.15	0.24	0.17	0.16	0.23	0.32	0.21	0.11	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA
raq_16	0.10	0.11	0.26	0.23	0.14	0.12	0.18	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA
raq_17	0.14	0.21	0.26	0.22	0.20	0.25	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA
raq_18	0.13	0.27	0.19	0.18	0.30	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA
raq_19	0.44	0.42	0.18	0.16	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA
raq_20	0.11	0.17	0.35	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA
raq_21	0.14	0.18	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA
raq_22	0.40	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA

• because the items use Likert scales, should use polychoric() function from the psych package

raq_poly <- psych::polychoric(raq_items_tib)
raq_poly

Call: psych::polychoric(x = raq_items_tib)
Polychoric correlations 
       rq_01 rq_02 rq_03 rq_04 rq_05 rq_06 rq_07 rq_08 rq_09 rq_10 rq_11
raq_01  1.00                                                            
raq_02  0.12  1.00                                                      
raq_03 -0.20 -0.13  1.00                                                
raq_04  0.24  0.14 -0.22  1.00                                          
raq_05  0.25  0.31 -0.28  0.35  1.00                                    
raq_06  0.18  0.37 -0.18  0.26  0.57  1.00                              
raq_07  0.12  0.28 -0.14  0.18  0.40  0.50  1.00                        
raq_08  0.25  0.20 -0.24  0.28  0.40  0.38  0.28  1.00                  
raq_09  0.09  0.43 -0.09  0.11  0.18  0.22  0.18  0.18  1.00            
raq_10  0.12  0.20 -0.11  0.20  0.35  0.44  0.31  0.20  0.12  1.00      
raq_11  0.21  0.17 -0.21  0.25  0.35  0.33  0.24  0.64  0.19  0.19  1.00
raq_12  0.17  0.10 -0.16  0.21  0.21  0.13  0.10  0.14  0.07  0.08  0.11
raq_13  0.12  0.25 -0.14  0.18  0.39  0.50  0.34  0.22  0.17  0.27  0.22
raq_14  0.13  0.22 -0.10  0.16  0.30  0.39  0.28  0.25  0.14  0.24  0.20
raq_15  0.12  0.21 -0.17  0.21  0.36  0.45  0.32  0.25  0.16  0.27  0.22
raq_16  0.19  0.11 -0.22  0.30  0.27  0.18  0.13  0.23  0.09  0.14  0.19
raq_17  0.18  0.19 -0.19  0.26  0.33  0.31  0.23  0.61  0.16  0.20  0.51
raq_18  0.13  0.29 -0.17  0.19  0.42  0.56  0.39  0.31  0.16  0.32  0.27
raq_19  0.12  0.43 -0.13  0.16  0.32  0.42  0.28  0.23  0.51  0.23  0.21
raq_20  0.23  0.14 -0.26  0.32  0.38  0.25  0.16  0.29  0.11  0.20  0.30
raq_21  0.25  0.18 -0.29  0.36  0.41  0.29  0.22  0.33  0.19  0.18  0.32
raq_22  0.14  0.38 -0.13  0.17  0.30  0.36  0.25  0.25  0.48  0.17  0.22
raq_23  0.09  0.43 -0.06  0.09  0.19  0.19  0.18  0.16  0.60  0.08  0.14
       rq_12 rq_13 rq_14 rq_15 rq_16 rq_17 rq_18 rq_19 rq_20 rq_21 rq_22
raq_12  1.00                                                            
raq_13  0.08  1.00                                                      
raq_14  0.08  0.30  1.00                                                
raq_15  0.08  0.32  0.26  1.00                                          
raq_16  0.17  0.17  0.09  0.12  1.00                                    
raq_17  0.08  0.20  0.19  0.24  0.20  1.00                              
raq_18  0.11  0.38  0.28  0.35  0.14  0.28  1.00                        
raq_19  0.08  0.29  0.24  0.26  0.15  0.22  0.33  1.00                  
raq_20  0.14  0.18  0.16  0.18  0.26  0.24  0.20  0.18  1.00            
raq_21  0.18  0.19  0.18  0.18  0.29  0.29  0.21  0.20  0.39  1.00      
raq_22  0.09  0.26  0.25  0.26  0.12  0.23  0.30  0.46  0.19  0.20  1.00
raq_23  0.06  0.15  0.14  0.17  0.11  0.15  0.14  0.49  0.13  0.16  0.45
[1]  1.00

 with tau of 
          1     2       3    4
raq_01 -2.0 -0.99 -0.0229 1.01
raq_02 -2.0 -1.03  0.0532 1.03
raq_03 -2.0 -0.99 -0.0093 0.99
raq_04 -2.0 -0.99  0.0044 1.00
raq_05 -1.9 -1.00  0.0356 0.97
raq_06 -2.0 -0.99  0.0132 0.97
raq_07 -2.0 -1.01 -0.0278 0.95
raq_08 -2.0 -1.00 -0.0239 1.01
raq_09 -2.1 -1.02 -0.0288 0.97
raq_10 -2.0 -0.98  0.0307 0.97
raq_11 -2.0 -0.98 -0.0219 1.04
raq_12 -2.0 -1.04 -0.0219 1.00
raq_13 -2.0 -1.00 -0.0180 1.02
raq_14 -2.0 -1.00 -0.0424 0.95
raq_15 -2.0 -1.03 -0.0678 0.95
raq_16 -2.0 -0.99  0.0063 1.01
raq_17 -2.0 -1.02  0.0122 1.02
raq_18 -2.0 -1.03  0.0015 1.02
raq_19 -2.0 -0.98  0.0112 0.99
raq_20 -2.0 -0.99 -0.0336 0.96
raq_21 -2.1 -0.99 -0.0073 1.02
raq_22 -2.1 -1.05  0.0210 1.03
raq_23 -2.1 -1.01 -0.0015 1.01

• matrix of correlations is stored in in a variable called rho, accessible with raq_poly$rho but we can store it in an object

raq_cor <- raq_poly$rho

psych::cor.plot(raq_cor, upper = FALSE)

• note items close to 0 - no correlation

• note items between $+/-$0.3

• note items greater than \(+/-\) 0.9 as those may be collinear or singular

• in this case, all questions correlate reasonably well and none are excessively large

Bartlett’s test and KMO test

Bartlett’s test of Sphericity

• tests whether the correlation matrix is significantly different from an identity matrix (whether the correlations are all 0

  • in FA, sample sizes are large, so the test will almost always be significant, but if it is not, then there is a problem

psych::cortest.bartlett(raq_cor, n = 2571)

$chisq
[1] 17387.52

$p.value
[1] 0

$df
[1] 253

• given large sample size, Bartlett’s test is highly significant, indicating there is not a significant problem

Kaiser-Meyer-Olkin (KMO)

• check for sampling adequacy

• KMO varies between 0 and 1 with 0 indicating FA is not appropriate

• values closer to 1 indicate compact patterns of correlations and FA should reveal distinct and reliable factors

  • Marvellous: values in the 0.90s

  • Meritorious: values in the 0.80s

  • Middling: values in the 0.70s

  • Mediocre: values in the 0.60s

  • Miserable: values in the 0.50s

psych::KMO(raq_cor)

Kaiser-Meyer-Olkin factor adequacy
Call: psych::KMO(r = raq_cor)
Overall MSA =  0.92
MSA for each item = 
raq_01 raq_02 raq_03 raq_04 raq_05 raq_06 raq_07 raq_08 raq_09 raq_10 raq_11 
  0.95   0.94   0.93   0.93   0.95   0.91   0.96   0.86   0.84   0.95   0.89 
raq_12 raq_13 raq_14 raq_15 raq_16 raq_17 raq_18 raq_19 raq_20 raq_21 raq_22 
  0.90   0.95   0.96   0.96   0.92   0.90   0.95   0.93   0.93   0.93   0.94 
raq_23 
  0.84 

• KMO statistic (Overall MSA) is 0.92 - well above the threshold of 0.5

• MSA for each individual item ranges from 0.84 - 0.96

Note

If you find KMO values below 0.5, consider removing that variable, but be sure to run the KMO statistic again without the removed variable. Also run the analysis with and without the variable to compare

Parallel analysis

• to determine how many factors to extract, run psych::fa.parallel()

• most likely arguments

  • n.obs() - need to tell the function the sample size (`n.obs = 2571`)

  • fm = “minres” - psych packages uses minimum residual (minres) by default

    • other options include principal axes (pa), alpha factoring (alpha), weighted least squares wls, minimum rank (minrank), or maximum likelihood (ml). Match this option to the one you’re going to use in the main factor analysis

  • fa = "both" - by default the function will tell the number of factors to extract, but also the number of components for PCA.

    • can change to fa = "fa” to see only the number of factors to extract. It is useful to look at both methods

  • use = “pairwise” - by default, missing data are handled using all complete pairwise observations to calculate the correlation coefficients

  • cor - default is the function assumes you are providing Pearson correlation coefficients, however, with ordinal variables (likert), use cor = "poly" (polychoric) and for binary, use tetrachoric cor = "tet"; with a mix of variable types, use cor ="mixed"

Code example

psych::fa.parallel(raq_items_tib, cor = "poly")

Parallel analysis suggests that the number of factors =  4  and the number of components =  4 

• or since we already stored polychoric correlations in raq_cor, we can just apply the function to that correlation matrix and specify the sample size

psych::fa.parallel(raq_cor, n.obs = 2571, fa = "fa")

Parallel analysis suggests that the number of factors =  4  and the number of components =  NA 

• eigenvalues represent the size of the factor

• factors are plotted on the x-axis with the eigenvalues on the y-axis

• each eigenvalue is compared to an eigenvalue from a simulated data set that has no underlying factors

  • essentially, we are asking if the factors are bigger than imaginary factor

  • factors that are bigger than their imaginary counterparts are retained

• eigenvalues for the observed factors are blue triangles connected by a blue line.

• the red line shows corresponding simulated data.

• we keep the number of factors that are above the red line, in this case, four

Quiz

Based on the parallel analysis that used principal components to compute the eiegenvalues, how many factors should be extracted?

• 4

Yes, fortunately this analysis agrees with the parallel analysis based on eigenvalues from factor analysis.

Factor Analysis

• we are now ready to run the FA, extracting four factors, using the psych::fa() function

my_fa_object <- psych::fa(r,    
                          n.obs = 2571,  
                          nfactors = 1,  
                          fm = "minres", 
                          rotate = "oblimin", 
                          scores = "regression", 
                          max.iter = 50, 
                          use = "pairwise", 
                          cor = "cor" 
                          )

• r -> the data being fed into the function (raq_items_tib or raq_cor)
• n.obs = 2571 as with parallel analysis, if we run the FA from the correlation matrix instead of the raw data, we must tell the function the sample size
• nfactors = 1 the number of factors to extract (default is 1)
• fm = "minres" method of factor analysis, typically leave the default
• rotate = "oblimin" method of factor rotation
• scores = "regression" method of computing factor scores. because we should use oblique rotation, change this argument to scores = "tenBerge"
• max.iter = 50 number of iterations. If you get a n error message about convergence, increase this number
• use = "pairwise" determines how missing values are treated, default is fine
• cor = "cor" same as defined for fa.parallel()

Factor rotation

factor rotation requires GPArotation package loaded

Code Example

• as with parallel analysis we can either feed the raw data into the function remembering to set cor = "poly" so the analysis is based on polychoric correlations
• or we can feed in the correlation matrix and sample size

raq_fa <- psych::fa(raq_items_tib, 
  nfactors = 4, 
  scores = "tenBerge", 
  cor = "poly"
  )
  raq_fa 

Factor Analysis using method =  minres
Call: psych::fa(r = raq_items_tib, nfactors = 4, scores = "tenBerge", 
    cor = "poly")
Standardized loadings (pattern matrix) based upon correlation matrix
         MR1   MR2   MR4   MR3   h2   u2 com
raq_01 -0.03  0.01  0.39  0.06 0.17 0.83 1.1
raq_02  0.25  0.48  0.02 -0.03 0.38 0.62 1.5
raq_03  0.00  0.01 -0.43 -0.03 0.20 0.80 1.0
raq_04  0.03 -0.02  0.56  0.00 0.33 0.67 1.0
raq_05  0.45 -0.01  0.39  0.02 0.54 0.46 2.0
raq_06  0.84  0.00 -0.01  0.03 0.73 0.27 1.0
raq_07  0.56  0.04  0.00  0.04 0.35 0.65 1.0
raq_08  0.00 -0.01 -0.01  0.88 0.75 0.25 1.0
raq_09 -0.07  0.81  0.00  0.03 0.62 0.38 1.0
raq_10  0.49 -0.05  0.09 -0.02 0.26 0.74 1.1
raq_11 -0.01  0.01  0.03  0.72 0.55 0.45 1.0
raq_12 -0.01  0.01  0.37 -0.07 0.11 0.89 1.1
raq_13  0.57  0.03  0.04 -0.03 0.34 0.66 1.0
raq_14  0.42  0.04  0.01  0.06 0.22 0.78 1.1
raq_15  0.48  0.03  0.03  0.05 0.29 0.71 1.0
raq_16 -0.05  0.02  0.51 -0.01 0.23 0.77 1.0
raq_17  0.03  0.02  0.00  0.68 0.49 0.51 1.0
raq_18  0.63  0.01 -0.02  0.07 0.43 0.57 1.0
raq_19  0.26  0.56  0.00 -0.01 0.50 0.50 1.4
raq_20  0.00  0.01  0.54  0.05 0.32 0.68 1.0
raq_21 -0.02  0.05  0.59  0.06 0.40 0.60 1.0
raq_22  0.19  0.52  0.03  0.05 0.41 0.59 1.3
raq_23 -0.08  0.79  0.02 -0.01 0.59 0.41 1.0

                       MR1  MR2  MR4  MR3
SS loadings           3.04 2.24 2.03 1.91
Proportion Var        0.13 0.10 0.09 0.08
Cumulative Var        0.13 0.23 0.32 0.40
Proportion Explained  0.33 0.24 0.22 0.21
Cumulative Proportion 0.33 0.57 0.79 1.00

 With factor correlations of 
     MR1  MR2  MR4  MR3
MR1 1.00 0.38 0.50 0.48
MR2 0.38 1.00 0.28 0.28
MR4 0.50 0.28 1.00 0.57
MR3 0.48 0.28 0.57 1.00

Mean item complexity =  1.1
Test of the hypothesis that 4 factors are sufficient.

df null model =  253  with the objective function =  6.79 with Chi Square =  17387.52
df of  the model are 167  and the objective function was  0.1 

The root mean square of the residuals (RMSR) is  0.01 
The df corrected root mean square of the residuals is  0.02 

The harmonic n.obs is  2571 with the empirical chi square  205.03  with prob <  0.024 
The total n.obs was  2571  with Likelihood Chi Square =  267.21  with prob <  1.3e-06 

Tucker Lewis Index of factoring reliability =  0.991
RMSEA index =  0.015  and the 90 % confidence intervals are  0.012 0.019
BIC =  -1044.08
Fit based upon off diagonal values = 1
Measures of factor score adequacy             
                                                   MR1  MR2  MR4  MR3
Correlation of (regression) scores with factors   0.93 0.91 0.88 0.92
Multiple R square of scores with factors          0.87 0.83 0.77 0.85
Minimum correlation of possible factor scores     0.73 0.66 0.54 0.70

• factors are labeled MR1, MR2, MR3, and MR4
• below the pattern matrix is information about how much variance each factor accounts for
  • Proportion var - MR1 accounts for 0.13 of the overall variance (13%), etc
  • Cumulative var is the proportion of the variance explained cumulatively by the factors - MR1 accounts for 0.13 and MR1 + MR2 together account for 0.13 + 0.10 = 0.23 (23%)
    • all four together account for 0.40 (40%)
  • Proportion explained is the proportion of the explained variance that is explained by a factor, so of the 40% of the variiance accounted for, 0.33 (33%) is attributable to MR1
• next, correlations between factors are displayed
  • all are non-zero, indicating the factors are correlated (and oblique rotation was appropriate)
  • all factors are positively and fairly strongly correlated to teach other meaning the latent constructs represented by the factors are related.
• several fit indices that tell us how the model fits the data
  • chi-square statistic for the model is given as the likelihood chi square, \(X^2=267.21, p<0.001\)
    • we want this to be non-significant but ours is highly significant. Our sample size is 2571 so small deviations from a good fit will be significant. This highlights the limitation of using significance to indicate model fit.
    • the Tucker Lewis Index of factoring reliability (TLI) is given as 0.991
    • RMSEA is 0.015 90% CI[0.012, 0.019]
    • RMSR is 0.01

Fit Indices

Good fit is (probably) indicated by

• combination of TLI > 0.96, and SRMR (RMSR in the output) < 0.06
• combination of RMSEA < 0.05 and SRMR < 0.09

The TLI is 0.99, which is greater than 0.96, and RMSR is 0.01 which is smaller than both 0.09 and 0.06. Furthermore, RMSEA is 0.015, which is less than 0.05. With the caveat that universal cut-offs need to be taken with a pinch of salt, it’s reasonable to conclude that the model has excellent fit.

Interpreting FA

• look at factor loadings (top of output in the pattern matrix) for each question on each factor to see which items load most heavily onto which factors
• this is difficult to interpret in the raw form, so use parameters::model_parameters() to sort items by their factor loadings and suppress factor loading sbelow a certain value

General form

parameters::model_parameters(my_fa_object, sort = TRUE, threshold = "max")

• my_fa_object is the factor analysis object containing the factor loadings.
• sort = "TRUE" sorts items by their factor loadings
• set threshold to a value above which we will show values. Default is maximum loading. To see all factor loadings, set threshold = NULL

parameters::model_parameters(raq_fa, sort = TRUE, threshold = "0.2") |>
  knitr::kable(digits = 2)

Variable	MR1	MR2	MR4	MR3	Complexity	Uniqueness
raq_06	0.84	NA	NA	NA	1.00	0.27
raq_18	0.63	NA	NA	NA	1.03	0.57
raq_13	0.57	NA	NA	NA	1.02	0.66
raq_07	0.56	NA	NA	NA	1.02	0.65
raq_10	0.49	NA	NA	NA	1.08	0.74
raq_15	0.48	NA	NA	NA	1.04	0.71
raq_05	0.45	NA	0.39	NA	1.97	0.46
raq_14	0.42	NA	NA	NA	1.06	0.78
raq_09	NA	0.81	NA	NA	1.02	0.38
raq_23	NA	0.79	NA	NA	1.02	0.41
raq_19	0.26	0.56	NA	NA	1.41	0.50
raq_22	NA	0.52	NA	NA	1.29	0.59
raq_02	0.25	0.48	NA	NA	1.54	0.62
raq_21	NA	NA	0.59	NA	1.04	0.60
raq_04	NA	NA	0.56	NA	1.01	0.67
raq_20	NA	NA	0.54	NA	1.02	0.68
raq_16	NA	NA	0.51	NA	1.02	0.77
raq_03	NA	NA	-0.43	NA	1.01	0.80
raq_01	NA	NA	0.39	NA	1.06	0.83
raq_12	NA	NA	0.37	NA	1.07	0.89
raq_08	NA	NA	NA	0.88	1.00	0.25
raq_11	NA	NA	NA	0.72	1.00	0.45
raq_17	NA	NA	NA	0.68	1.00	0.51

• Now we can see patterns in the questions that load onto the same factors
• Items that load highly on MR1 seem to be items that relate to fear of computers
  • raq_05: I don’t understand statistics (also loads highly onto MR4)
  • raq_06: I have little experience of computers
  • raq_07: All computers hate me
  • raq_10: Computers are useful only for playing games
  • raq_13: I worry that I will cause irreparable damage because of my incompetence with computers
  • raq_14: Computers have minds of their own and deliberately go wrong whenever I use them
  • raq_15: Computers are out to get me
  • raq_18: R always crashes when I try to use it
• Items that load onto MR2 relate to fear of peer/social evaluation
  • raq_02: My friends will think I’m stupid for not being able to cope with R
  • raq_09: My friends are better at statistics than me
  • raq_19: Everybody looks at me when I use R
  • raq_22: My friends are better at R than I am
  • raq_23: If I am good at statistics people will think I am a nerd
• Questions that load onto MR4 relate to fear of statistics
  • raq_01: Statistics make me cry
  • raq_03: Standard deviations excite me
  • raq_04: I dream that Pearson is attacking me with correlation coefficients
  • raq_05: I don’t understand statistics
  • raq_12: People try to tell you that R makes statistics easier to understand but it doesn’t
  • raq_16: I weep openly at the mention of central tendency
  • raq_20: I can’t sleep for thoughts of eigenvectors
  • raq_21: I wake up under my duvet thinking that I am trapped under a normal distribution
• questions that load onto MR3 relate to fear of math
  • raq_08: I have never been good at mathematics
  • raq_11: I did badly at mathematics at school
  • raq_17: I slip into a coma whenever I see an equation

Analysis seems to reveal that the questionnaire is composed of four subscales: fear of statistics, fear of computers, fear of maths, fear of negative peer evaluation.

• two possibilities:
  • the RAQ failed to measure what it set out to measure -> R anxiety but instead measures related constructs
  • these four constructs are subcomponents of R anxiety
• However, the factor analysis does not indicate which of these is true.

Reliability Analysis

McDonald’s \(\omega_t\) and \(\omega_h\)

• if items are all scored in the same direction, we can select the variables on a particular subscale and pipe them into omega() functions in the psych package

my_omg <- psych::omega(
    my_tibble
    nfactors = 1,
    fm = "minres",
    key = c(1, 1, -1, 1, 1 … 1),
    rotate = "oblimin",
    poly = FALSE
  )

my_omg

name to give the object that stores the results

my_tibble

name of the tibble containing your data

Code Example

• need to recreate the original FA
• arguments will be the same as they were set for the fa
• the key argument allows us to reverse item scoring on the fly
• supply the key argument with a vector of 1s and -1s that is the same length as the number of variables being fed into the omega() function
• for RAQ, we have 23 items with the third being reverse coded
• entering the items in order into omega() gives

key = c(1, 1, -1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1)

or

key = c(1, 1, -1, rep(1, 20))

raq_omg <- psych::omega(raq_items_tib,
                        nfactors = 4,
                        fm = "minres",
                        key = c(1, 1, -1, rep(1, 20)),
                        poly = TRUE
                        )

raq_omg

Omega 
Call: omegah(m = m, nfactors = nfactors, fm = fm, key = key, flip = flip, 
    digits = digits, title = title, sl = sl, labels = labels, 
    plot = plot, n.obs = n.obs, rotate = rotate, Phi = Phi, option = option, 
    covar = covar)
Alpha:                 0.88 
G.6:                   0.89 
Omega Hierarchical:    0.68 
Omega H asymptotic:    0.75 
Omega Total            0.9 

Schmid Leiman Factor loadings greater than  0.2 
           g   F1*   F2*   F3*   F4*   h2   u2   p2
raq_01  0.32              0.26       0.17 0.83 0.57
raq_02  0.37        0.43             0.38 0.62 0.37
raq_03- 0.34              0.29       0.20 0.80 0.56
raq_04  0.43              0.38       0.33 0.67 0.56
raq_05  0.62  0.32        0.27       0.54 0.46 0.70
raq_06  0.61  0.60                   0.73 0.27 0.51
raq_07  0.44  0.39                   0.35 0.65 0.54
raq_08  0.62                    0.61 0.75 0.25 0.51
raq_09  0.32        0.73             0.62 0.38 0.17
raq_10  0.37  0.35                   0.26 0.74 0.53
raq_11  0.54                    0.50 0.55 0.45 0.54
raq_12  0.22              0.25       0.11 0.89 0.44
raq_13  0.42  0.40                   0.34 0.66 0.51
raq_14  0.36  0.30                   0.22 0.78 0.59
raq_15  0.41  0.34                   0.29 0.71 0.59
raq_16  0.34              0.34       0.23 0.77 0.49
raq_17  0.52                    0.47 0.49 0.51 0.55
raq_18  0.48  0.44                   0.43 0.57 0.54
raq_19  0.43        0.51             0.50 0.50 0.37
raq_20  0.43              0.36       0.32 0.68 0.58
raq_21  0.49              0.40       0.40 0.60 0.59
raq_22  0.41        0.46             0.41 0.59 0.41
raq_23  0.30        0.71             0.59 0.41 0.15

With Sums of squares  of:
   g  F1*  F2*  F3*  F4* 
4.40 1.39 1.71 0.85 0.86 

general/max  2.58   max/min =   2.01
mean percent general =  0.49    with sd =  0.13 and cv of  0.26 
Explained Common Variance of the general factor =  0.48 

The degrees of freedom are 167  and the fit is  0.1 
The number of observations was  2571  with Chi Square =  267.21  with prob <  1.3e-06
The root mean square of the residuals is  0.01 
The df corrected root mean square of the residuals is  0.02
RMSEA index =  0.015  and the 10 % confidence intervals are  0.012 0.019
BIC =  -1044.08

Compare this with the adequacy of just a general factor and no group factors
The degrees of freedom for just the general factor are 230  and the fit is  2.39 
The number of observations was  2571  with Chi Square =  6122.42  with prob <  0
The root mean square of the residuals is  0.1 
The df corrected root mean square of the residuals is  0.11 

RMSEA index =  0.1  and the 10 % confidence intervals are  0.098 0.102
BIC =  4316.45 

Measures of factor score adequacy             
                                                 g  F1*  F2*   F3*  F4*
Correlation of scores with factors            0.84 0.76 0.87  0.67 0.74
Multiple R square of scores with factors      0.71 0.57 0.75  0.44 0.55
Minimum correlation of factor score estimates 0.42 0.14 0.51 -0.11 0.10

 Total, General and Subset omega for each subset
                                                 g  F1*  F2*  F3*  F4*
Omega total for total scores and subscales    0.90 0.83 0.80 0.69 0.81
Omega general for total scores and subscales  0.68 0.48 0.23 0.38 0.43
Omega group for total scores and subscales    0.18 0.35 0.56 0.31 0.38

• note the table of factor loadings and that raq_03- is labeled with a minus to indicate it is reverse coded

• column labeled gshows the loading of each item on the general factor

  • if any items load poorly, then a common factor model isn’t appropriate
  • all items here have a factor loading far enough from zero that a general factor model is appropriate

• Columns F1-F4 show the loadings of each item on the four factors we extracted

  • these values differ from the original factor analysis because this one includes a general factor
  • the patterns of item loadings to factors follow the same pattern as the original FA

• at the top of the text output are reliability estimates for the general factor, including

  • Chronbach’s \(\alpha=0.88\)
  • \(\omega_h=0.68\)
  • \(\omega_t=0.9\)

• \(\omega_h\) is a measure of how much the items reflect a single construct, and a value of 0.68 suggests they do but there is still a lot of unexplained variance in the general factor

• further down in the output, we see that only 48% of the variance in the common factor is explained by the items

• \(\omega_t\) is the total reliability and 0.90 is high, suggesting scores are reliable

• next are two sets of model fit stats

• the first set are for the model that has four factors and repeat the nformation from the original EFA

  • chi-square is significant, \(X^2= 267.21, p<0.001\), which is a bad thing but unsurprising given the sample size
  • RMSR = 0.01
  • RMSEA = 0.02 90% CI[0.01-0.02]

• Next is the same information but for the model that contains only the general factor and not the four sub-factors

  • the fit gets worse as shown by
    • larger and more significant chi-square, $X^2=6122.42, p<0.001$
    • larger RMSR=0.10
    • larger RMSEA=0.1090% CI[0.10, 0.10]

• all this tells us that the model that characterizes the RAQ in terms of four factors is a better fit of the data than a model that characterises it as a single factor

• finally, under the Total, General, and Subset omega for each subset, we get the \(\omega_t\) (labeled omega total) and \(\omega_h\) (labeled omega general) for the general factor (column g) and for the subfactors.

• values for the general factor repeat the information at tht e start of the output

• the values for the subfactors are particularly relvant for \(\omega_t\) because it represents the total reliability of the scores, so these values tell us the total reliability of the scores from the underlying subscales

  • for anxiety related to computers (F1) we have \(\omega_t=0.83\)
  • anxiety around peer or social evaluation (F2) $_t=0.80
  • anxiety around statistics (F3) \(\omega_t=0.69\)
  • anxiety around maths (F4) \(\omega_t=0.81\)

• scores from ach subscale are reliable, although somewhat less so for anxiety around statistics

Cronbach’s \(\alpha\)

• Lots of reasons not to use Cronbach’s \(\alpha\) (see the book for details)
• if Cronbach’s \(\alpha\) is needed, it must be computed on the individual subscales
  • Anxiety related to computers: raq_06, raq_07, raq_10, raq_13, raq_14, raq_15 and raq_18
  • Anxiety around peer or social evaluation: raq_02, raq_09, raq_19, raq_22, and raq_2
  • Anxiety around statistics: raq_01, raq_03 (reverse scored), raq_04, raq_05, raq_12, raq_16, raq_20, and raq_21
  • Anxiety around maths: raq_08, raq_11 and raq_17
• pipe the variables for each subscale into psych::alpha() function

Code example for fear of computers

• example excludes raq_05, which makes more sense on the fear of statistics factor [See github issue]

raq_tib |> 
  dplyr::select(raq_06, raq_07, raq_10, raq_13, raq_14, raq_15, raq_18) |> 
  psych::alpha()

Reliability analysis   
Call: psych::alpha(x = dplyr::select(raq_tib, raq_06, raq_07, raq_10, 
    raq_13, raq_14, raq_15, raq_18))

  raw_alpha std.alpha G6(smc) average_r S/N    ase mean   sd median_r
      0.77      0.77    0.75      0.32 3.3 0.0069  3.5 0.64     0.29

    95% confidence boundaries 
         lower alpha upper
Feldt     0.75  0.77  0.78
Duhachek  0.76  0.77  0.78

 Reliability if an item is dropped:
       raw_alpha std.alpha G6(smc) average_r S/N alpha se  var.r med.r
raq_06      0.70      0.70    0.66      0.28 2.3   0.0092 0.0015  0.28
raq_07      0.74      0.74    0.71      0.32 2.9   0.0079 0.0075  0.29
raq_10      0.75      0.75    0.73      0.34 3.1   0.0075 0.0068  0.32
raq_13      0.74      0.74    0.71      0.32 2.9   0.0079 0.0074  0.29
raq_14      0.76      0.76    0.73      0.35 3.2   0.0073 0.0065  0.32
raq_15      0.75      0.75    0.72      0.33 3.0   0.0076 0.0076  0.31
raq_18      0.73      0.73    0.70      0.31 2.7   0.0082 0.0063  0.29

 Item statistics 
          n raw.r std.r r.cor r.drop mean   sd
raq_06 2571  0.79  0.79  0.77   0.68  3.5 0.99
raq_07 2571  0.65  0.65  0.56   0.49  3.5 1.00
raq_10 2571  0.59  0.59  0.48   0.42  3.5 1.00
raq_13 2571  0.64  0.64  0.55   0.48  3.5 0.98
raq_14 2571  0.57  0.57  0.45   0.39  3.5 1.00
raq_15 2571  0.61  0.61  0.51   0.44  3.5 0.99
raq_18 2571  0.67  0.68  0.60   0.53  3.5 0.97

Non missing response frequency for each item
          1    2    3    4    5 miss
raq_06 0.02 0.14 0.35 0.33 0.17    0
raq_07 0.02 0.13 0.33 0.34 0.17    0
raq_10 0.02 0.14 0.35 0.32 0.17    0
raq_13 0.02 0.14 0.33 0.35 0.15    0
raq_14 0.02 0.13 0.33 0.35 0.17    0
raq_15 0.02 0.13 0.32 0.35 0.17    0
raq_18 0.02 0.13 0.35 0.35 0.15    0

• value at the top is Cronbach’s \(\alpha\), with the 95% CI below.

• looking for between 0.70 and 0.80, in this case Cronbach’s \(\alpha\)=0.77 [0.75, 0.78] indicating good reliability

• next is a table of statistics for the scale if we deleted each item in turn

• the values in the column raw_alpha are the values of the overall \(\alpha\)

• we are looking for a change in Cronbach’s \(\alpha\) (0.77)

  • if values are greater than 0.77, then reliability would have improved if the item were removed - not the case here

• the table labeled item statistics shows, in raw.r, the correlations between each item and the total score from the scale - item-total correlations

  • there is a problem with this statistic in that the item is included in the scale total, which inflates the overall correlation.
  • we want these correlations to be computed without the item in question, and these values are in r.drop
  • in a reliable scale all items should correlate with the total, so we’re looking for items that don’t correlate with the overall score from the subscale. If any values of r.drop are elss than 0.3, we have problems becasuse that means an item does not correlate well with the subscale
    • 0.3 is ‘reasonable’ - use your judgement

• the final table tells us what percentage of people gave each response to each of the items, which is useful to make sure everyone in the sample is not giving the same response.

  • usually, if everyone gives the same response, the item will have poor reliability statistics
  • for this subscale, few people responded with a 1 on any of the items suggesting that no one is feeling the love for computers or that the items are doing a poor job of eliciting those extreme responses

Code example for fear of peer/social evaluation

raq_tib |> 
  dplyr::select(raq_02, raq_09, raq_19, raq_22, raq_23)  |> 
  psych::alpha()

Reliability analysis   
Call: psych::alpha(x = dplyr::select(raq_tib, raq_02, raq_09, raq_19, 
    raq_22, raq_23))

  raw_alpha std.alpha G6(smc) average_r S/N    ase mean   sd median_r
      0.78      0.78    0.75      0.42 3.6 0.0067  3.5 0.72     0.41

    95% confidence boundaries 
         lower alpha upper
Feldt     0.77  0.78   0.8
Duhachek  0.77  0.78   0.8

 Reliability if an item is dropped:
       raw_alpha std.alpha G6(smc) average_r S/N alpha se  var.r med.r
raq_02      0.77      0.77    0.71      0.45 3.3   0.0075 0.0027  0.43
raq_09      0.72      0.72    0.67      0.40 2.6   0.0089 0.0011  0.40
raq_19      0.74      0.74    0.69      0.42 2.8   0.0084 0.0049  0.40
raq_22      0.76      0.76    0.71      0.44 3.1   0.0078 0.0038  0.42
raq_23      0.73      0.73    0.67      0.41 2.7   0.0086 0.0018  0.40

 Item statistics 
          n raw.r std.r r.cor r.drop mean   sd
raq_02 2571  0.68  0.69  0.55   0.49  3.5 0.97
raq_09 2571  0.77  0.77  0.70   0.62  3.5 0.99
raq_19 2571  0.74  0.74  0.64   0.57  3.5 1.00
raq_22 2571  0.70  0.71  0.59   0.52  3.5 0.96
raq_23 2571  0.76  0.76  0.68   0.60  3.5 0.98

Non missing response frequency for each item
          1    2    3    4    5 miss
raq_02 0.02 0.13 0.37 0.33 0.15    0
raq_09 0.02 0.13 0.33 0.34 0.17    0
raq_19 0.02 0.14 0.34 0.34 0.16    0
raq_22 0.02 0.13 0.36 0.34 0.15    0
raq_23 0.02 0.14 0.34 0.34 0.16    0

• good overall reliability (\(\alpha=0.78 [o.77, 0.80]\))
• no items improve the value if they are dropped
• item correlations with the total are all good
• again we have issues with the items not eliciting extremely low responses

Code example for fear of maths

raq_tib |> 
  dplyr::select(raq_08, raq_11, raq_17)  |> 
  psych::alpha()

Reliability analysis   
Call: psych::alpha(x = dplyr::select(raq_tib, raq_08, raq_11, raq_17))

  raw_alpha std.alpha G6(smc) average_r S/N    ase mean   sd median_r
      0.77      0.77     0.7      0.53 3.4 0.0078  3.5 0.81     0.55

    95% confidence boundaries 
         lower alpha upper
Feldt     0.76  0.77  0.79
Duhachek  0.76  0.77  0.79

 Reliability if an item is dropped:
       raw_alpha std.alpha G6(smc) average_r S/N alpha se var.r med.r
raq_08      0.63      0.63    0.47      0.47 1.7    0.014    NA  0.47
raq_11      0.71      0.71    0.55      0.55 2.4    0.012    NA  0.55
raq_17      0.74      0.74    0.58      0.58 2.8    0.010    NA  0.58

 Item statistics 
          n raw.r std.r r.cor r.drop mean   sd
raq_08 2571  0.86  0.86  0.75   0.66  3.5 0.98
raq_11 2571  0.82  0.82  0.68   0.60  3.5 0.99
raq_17 2571  0.81  0.81  0.65   0.57  3.5 0.97

Non missing response frequency for each item
          1    2    3    4    5 miss
raq_08 0.02 0.14 0.33 0.35 0.16    0
raq_11 0.02 0.14 0.33 0.36 0.15    0
raq_17 0.02 0.13 0.35 0.34 0.15    0

• fairly high reliability (\(\alpha=0.77 [0.76, 0.79]\))
• no items improve value if they are dropped
• item correlations with the total subscale are all good
• still issues with items not eliciting low responses

Code example for fear of statistics

• the fear of statistics subscale contains raq_3, which is reverse scored so we need to include the keys argument within the function
• note that in the omega() function, the argument is key, but in the alpha() function, the argument is keys

raq_tib |> 
  dplyr::select(raq_01, raq_03, raq_04, raq_05, raq_12, raq_16, raq_20, raq_21)  |> 
  psych::alpha(keys = c(1, -1, 1, 1, 1, 1, 1, 1))

Reliability analysis   
Call: psych::alpha(x = dplyr::select(raq_tib, raq_01, raq_03, raq_04, 
    raq_05, raq_12, raq_16, raq_20, raq_21), keys = c(1, -1, 
    1, 1, 1, 1, 1, 1))

  raw_alpha std.alpha G6(smc) average_r S/N    ase mean   sd median_r
      0.71      0.54    0.56      0.13 1.2 0.0087  3.4 0.57      0.2

    95% confidence boundaries 
         lower alpha upper
Feldt     0.69  0.71  0.72
Duhachek  0.69  0.71  0.72

 Reliability if an item is dropped:
        raw_alpha std.alpha G6(smc) average_r  S/N alpha se  var.r med.r
raq_01       0.69      0.49    0.52      0.12 0.95   0.0092 0.0520  0.20
raq_03-      0.69      0.69    0.66      0.24 2.19   0.0094 0.0051  0.23
raq_04       0.67      0.44    0.48      0.10 0.79   0.0100 0.0461  0.18
raq_05       0.66      0.44    0.47      0.10 0.78   0.0102 0.0421  0.18
raq_12       0.71      0.51    0.54      0.13 1.04   0.0088 0.0542  0.23
raq_16       0.68      0.48    0.51      0.11 0.91   0.0095 0.0496  0.20
raq_20       0.67      0.46    0.49      0.11 0.84   0.0099 0.0447  0.19
raq_21       0.66      0.44    0.47      0.10 0.78   0.0103 0.0415  0.19

 Item statistics 
           n raw.r std.r r.cor r.drop mean   sd
raq_01  2571  0.52  0.52  0.39   0.33  3.5 0.99
raq_03- 2571  0.54 -0.12 -0.46   0.36  2.5 0.99
raq_04  2571  0.61  0.62  0.56   0.45  3.5 0.99
raq_05  2571  0.64  0.62  0.58   0.48  3.5 1.00
raq_12  2571  0.46  0.47  0.31   0.27  3.5 0.98
raq_16  2571  0.55  0.55  0.44   0.37  3.5 0.98
raq_20  2571  0.61  0.59  0.52   0.44  3.5 1.00
raq_21  2571  0.64  0.63  0.58   0.49  3.5 0.98

Non missing response frequency for each item
          1    2    3    4    5 miss
raq_01 0.02 0.14 0.33 0.35 0.16    0
raq_03 0.02 0.14 0.34 0.34 0.16    0
raq_04 0.02 0.14 0.34 0.34 0.16    0
raq_05 0.03 0.13 0.35 0.32 0.16    0
raq_12 0.02 0.12 0.34 0.35 0.16    0
raq_16 0.02 0.14 0.34 0.34 0.16    0
raq_20 0.02 0.14 0.33 0.35 0.17    0
raq_21 0.02 0.14 0.34 0.35 0.15    0

• note that raq_03- has a minus to indicate reverse scoring
• acceptable overall reliability (\(\alpha=0.71 [0.69, 0.72]\))
• no items improve the value if they are dropped
• item correlations with the total subscale are ok (0.27-0.49)
• issue with items not eliciting extreme responses

References

Field, Andy. 2023. “Discovr: Interactive Tutorials and Data for "Discovering Statistics Using r and RStudio".”

Wickham, Hadley. 2016. Ggplot2: Elegant Graphics for Data Analysis. Springer-Verlag New York. https://ggplot2.tidyverse.org.